3 4 Divided By 1 8 In Fraction Form
faraar
Sep 10, 2025 · 6 min read
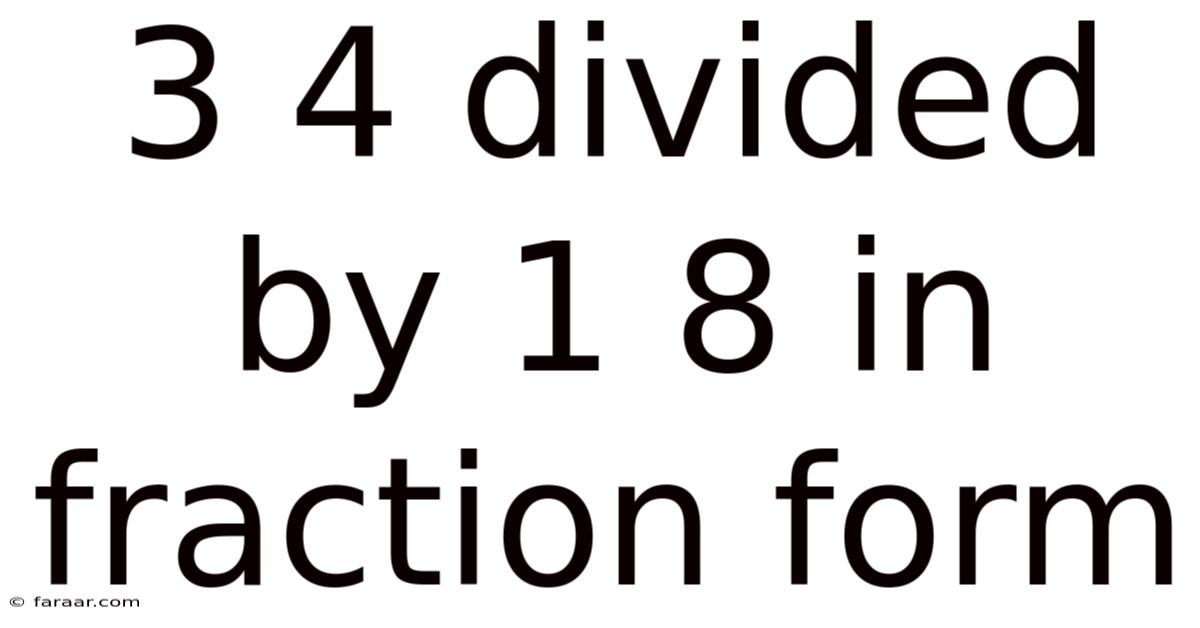
Table of Contents
Diving Deep into Fractions: Solving 3/4 Divided by 1/8
Understanding fractions can sometimes feel like navigating a maze, especially when division enters the picture. This comprehensive guide will walk you through solving the fraction problem 3/4 divided by 1/8, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common misconceptions. By the end, you'll not only know the answer but also possess a deeper understanding of fraction division that you can apply to more complex problems.
Introduction: Why Fraction Division Matters
Fraction division is a fundamental concept in mathematics with real-world applications in various fields. From calculating ingredient ratios in cooking to determining the portion of a whole in construction projects, mastering this skill is essential for both academic success and practical problem-solving. This article focuses on the specific problem of 3/4 divided by 1/8, using this example to illustrate the broader principles of dividing fractions. We'll explore different methods, explain the reasoning behind each step, and offer a clear, concise solution. Understanding this seemingly simple problem lays the groundwork for tackling more advanced mathematical concepts.
Method 1: The "Keep, Change, Flip" Method (Inversion)
This is arguably the most popular and straightforward method for dividing fractions. It's based on the principle that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. Let's apply this to our problem:
1. Keep the first fraction: We keep 3/4 as it is.
2. Change the division sign: We change the division symbol (÷) to a multiplication symbol (×).
3. Flip the second fraction: We find the reciprocal of 1/8, which is 8/1.
Therefore, our problem transforms from: 3/4 ÷ 1/8 to: 3/4 × 8/1
4. Multiply the numerators and denominators: We multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 × 8) / (4 × 1) = 24/4
5. Simplify the fraction: We simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4:
24/4 = 6
Therefore, 3/4 divided by 1/8 equals 6.
Method 2: Using Common Denominators
This method utilizes the concept of finding a common denominator for both fractions before performing the division. While it might seem more complex than the "keep, change, flip" method, understanding this approach provides a deeper insight into the underlying principles of fraction manipulation.
1. Find a common denominator: The least common denominator (LCD) for 4 and 8 is 8.
2. Convert fractions to equivalent fractions with the common denominator:
- 3/4 becomes 6/8 (multiply both numerator and denominator by 2)
- 1/8 remains 1/8
3. Rewrite the division problem: The problem now becomes 6/8 ÷ 1/8
4. Perform the division: Dividing fractions with the same denominator simply involves dividing the numerators:
6/8 ÷ 1/8 = 6 ÷ 1 = 6
Therefore, 3/4 divided by 1/8 equals 6. This method highlights that when dividing fractions with the same denominator, the result is simply the division of the numerators.
Visualizing the Problem: A Real-World Analogy
Let's imagine you have a pizza cut into 4 equal slices (3/4 of a pizza). You want to know how many 1/8 slices are in 3/4 of a pizza.
Imagine dividing each of your 3/4 slices into two smaller slices. Each of the original 1/4 slices is now divided into two 1/8 slices. This means that the 3/4 of the pizza consists of 6 pieces of 1/8 size each. Therefore, there are 6 slices of 1/8 size in 3/4 of a pizza. This visual representation confirms our mathematical calculation.
The Mathematical Explanation Behind Fraction Division
The "keep, change, flip" method isn't just a trick; it's derived from the fundamental principles of division and reciprocals. Dividing by a fraction is equivalent to multiplying by its multiplicative inverse (reciprocal). The reciprocal of a fraction a/b is b/a. This is because:
(a/b) ÷ (c/d) = (a/b) × (d/c) = (a × d) / (b × c)
This formula underpins the "keep, change, flip" method, showing that it's a concise and efficient way to perform fraction division. It avoids the sometimes more cumbersome process of finding a common denominator, especially when dealing with larger or more complex fractions.
Addressing Common Misconceptions
A frequent mistake is simply dividing the numerators and the denominators separately without applying the "keep, change, flip" method or finding a common denominator. This will yield an incorrect result. For instance, incorrectly dividing 3/4 by 1/8 as 3/32 would be a common error. Remember, dividing fractions involves a more intricate process than simply dividing the numerators and denominators individually.
Extending the Concept: More Complex Problems
The principles learned from solving 3/4 ÷ 1/8 can be readily applied to more complex fraction division problems. The "keep, change, flip" method remains an effective and efficient strategy. For example, let's consider 5/6 ÷ 2/3:
- Keep: 5/6
- Change: ÷ becomes ×
- Flip: 2/3 becomes 3/2
The problem becomes: 5/6 × 3/2 = (5 × 3) / (6 × 2) = 15/12 = 5/4
This demonstrates the versatility and power of the "keep, change, flip" method. Remember to always simplify your final answer to its lowest terms.
Frequently Asked Questions (FAQs)
Q: Why does the "keep, change, flip" method work?
A: The method is based on the mathematical property of reciprocals. Dividing by a fraction is equivalent to multiplying by its reciprocal. This simplifies the division process, making it easier to solve.
Q: Can I always use the "keep, change, flip" method?
A: Yes, the "keep, change, flip" method is a universally applicable method for dividing fractions. It provides a consistent and reliable approach to solving any fraction division problem.
Q: What if the fractions have different denominators?
A: Even if fractions have different denominators, the "keep, change, flip" method still applies. You only need to simplify the resulting fraction after multiplying the numerators and denominators. You do not need to find a common denominator before applying the method.
Q: What if one of the numbers is a whole number?
A: Treat the whole number as a fraction with a denominator of 1. For instance, 2 ÷ 1/3 would become 2/1 ÷ 1/3, then following the "keep, change, flip" method.
Q: How can I check my answer?
A: You can check your answer by multiplying the quotient (the result of the division) by the divisor (the second fraction). If the result equals the dividend (the first fraction), your answer is correct. For example, 6 × (1/8) = 6/8 = 3/4, confirming our answer for 3/4 ÷ 1/8 = 6.
Conclusion: Mastering Fraction Division
This in-depth exploration of 3/4 divided by 1/8 has not only provided the solution (6) but also equipped you with a deeper understanding of fraction division. By understanding both the "keep, change, flip" method and the common denominator method, you possess multiple strategies for tackling various fraction division problems. Remember to practice regularly; the more you work with fractions, the more comfortable and confident you'll become in manipulating them. This foundational knowledge will serve as a strong base for more advanced mathematical concepts you'll encounter in the future. Mastering fractions is a crucial step towards mathematical fluency and success in various academic and real-world scenarios.
Latest Posts
Latest Posts
-
How To Find Zeros In A Polynomial Function
Sep 10, 2025
-
Given 2 And 4 Are Vertical Angles
Sep 10, 2025
-
What Is 5 5 In Fraction Form
Sep 10, 2025
-
Each Pair Of Figures Is Similar Find The Missing Side
Sep 10, 2025
-
The Population Of A Town Increased From 7800 To 8775
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 1 8 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.