3/4 Divided By 1/8 In Fraction
faraar
Sep 20, 2025 · 5 min read
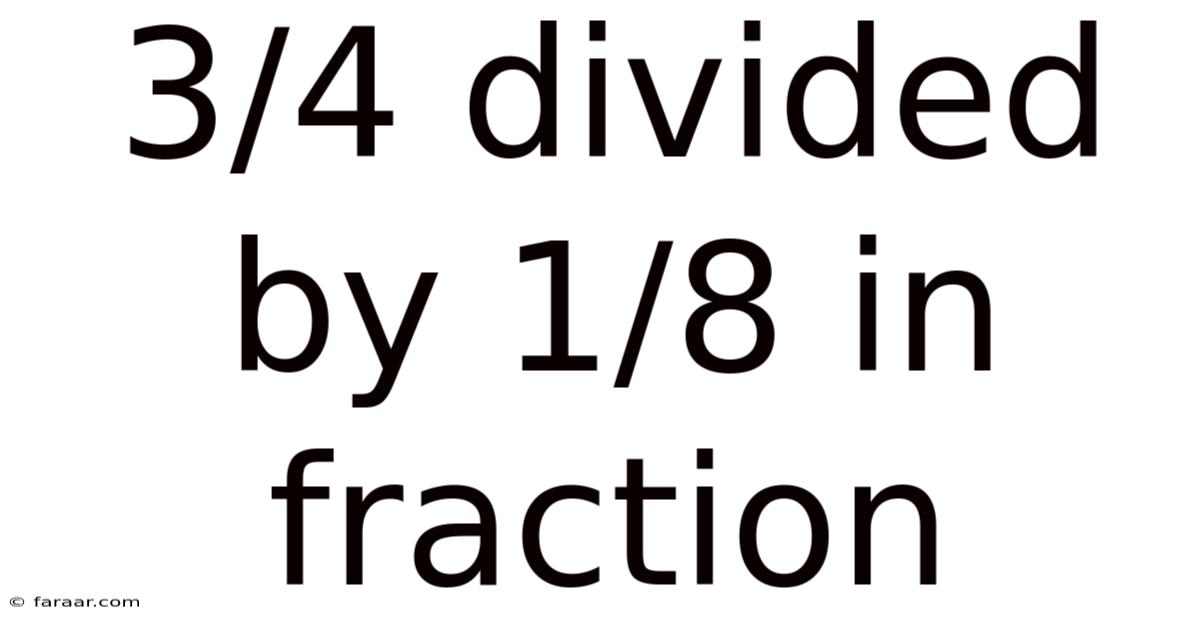
Table of Contents
Mastering Fractions: A Deep Dive into 3/4 Divided by 1/8
Understanding fractions is fundamental to grasping many mathematical concepts. This article provides a comprehensive guide to dividing fractions, specifically addressing the problem of 3/4 divided by 1/8. We'll explore the process step-by-step, delve into the underlying mathematical principles, and address common misconceptions. By the end, you'll not only be able to solve this particular problem but also confidently tackle any fraction division problem.
Introduction: Why Fraction Division Matters
Dividing fractions might seem daunting at first, but it's a crucial skill with wide-ranging applications. From calculating ingredient ratios in cooking to solving complex physics problems, mastering fraction division empowers you to tackle a variety of challenges effectively. This article focuses on the specific problem of 3/4 divided by 1/8, but the methods explained are universally applicable. We will cover the "Keep, Change, Flip" method, explore the underlying principles of reciprocal multiplication, and address frequently asked questions to ensure a thorough understanding.
Understanding the Problem: 3/4 ÷ 1/8
The problem we're tackling is: 3/4 ÷ 1/8. This reads as "three-quarters divided by one-eighth." Before we jump into the solution, let's clarify what division actually represents. In this context, division asks the question: "How many times does 1/8 fit into 3/4?" This interpretation is key to understanding the logic behind the solution.
Method 1: The "Keep, Change, Flip" Method
This popular method provides a quick and easy way to divide fractions. Here's how it works:
- Keep: Keep the first fraction (the dividend) exactly as it is: 3/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – this is called finding the reciprocal. The reciprocal of 1/8 is 8/1 (or simply 8).
So, our problem transforms from 3/4 ÷ 1/8 to 3/4 × 8/1.
-
Multiply: Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 × 8) / (4 × 1) = 24/4
-
Simplify: Finally, simplify the resulting fraction. 24/4 simplifies to 6.
Therefore, 3/4 divided by 1/8 equals 6.
Method 2: Visualizing the Division
Imagine you have a pizza cut into four equal slices. You possess three of these slices (3/4 of a pizza). Now, imagine each of these slices is further divided into two smaller, equal pieces (creating eighths). You now have 6 smaller pieces (6/8, which simplifies to 3/4). Each of those smaller pieces represents 1/8 of the original pizza. Consequently, there are six 1/8 slices in your original 3/4. This visual representation helps solidify the understanding of the mathematical process.
Method 3: Finding a Common Denominator
This method is less efficient for this particular problem but helps illustrate the underlying concept of division. To divide fractions using a common denominator, follow these steps:
-
Find a common denominator: The least common multiple of 4 and 8 is 8.
-
Convert fractions to have a common denominator:
- 3/4 becomes 6/8 (multiply both numerator and denominator by 2)
- 1/8 remains 1/8
-
Divide the numerators: Now, divide the numerator of the first fraction by the numerator of the second fraction: 6 ÷ 1 = 6.
Therefore, 3/4 divided by 1/8 equals 6, confirming the result from the previous methods.
The Mathematical Principle: Reciprocal Multiplication
The "Keep, Change, Flip" method is a shortcut for a more fundamental mathematical principle: dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and denominator. For example, the reciprocal of a/b is b/a.
This principle is rooted in the definition of division. Dividing by a number is the same as multiplying by its multiplicative inverse (reciprocal). This is true for all numbers, including fractions. Therefore, 3/4 ÷ 1/8 = 3/4 × 8/1.
Addressing Common Misconceptions
- Incorrectly flipping the first fraction: Remember, you only flip the second fraction (the divisor).
- Forgetting to simplify: Always simplify the resulting fraction to its lowest terms. Leaving the answer as 24/4 is mathematically correct but not considered fully simplified.
- Confusing multiplication and division: Understand the distinction between multiplying and dividing fractions. While the "Keep, Change, Flip" method uses multiplication, it's fundamentally a division problem.
Expanding the Concept: More Complex Fraction Division
The principles outlined above apply to all fraction division problems, regardless of their complexity. For instance, consider the problem 5/6 ÷ 2/3:
- Keep: 5/6
- Change: ×
- Flip: 3/2
- Multiply: (5 × 3) / (6 × 2) = 15/12
- Simplify: 15/12 simplifies to 5/4 or 1 ¼.
Frequently Asked Questions (FAQ)
-
Q: What if the divisor is a whole number? A: Simply write the whole number as a fraction with a denominator of 1 (e.g., 5 becomes 5/1) and then apply the "Keep, Change, Flip" method.
-
Q: What if both the dividend and divisor are mixed numbers? A: Convert the mixed numbers into improper fractions before applying the division method. For instance, 1 1/2 ÷ 2 1/4 would be converted to 3/2 ÷ 9/4, then solved as 3/2 × 4/9 = 12/18 = 2/3.
-
Q: Why does flipping the fraction work? A: Flipping the fraction is a shortcut for multiplying by the reciprocal, which is based on the fundamental properties of division and multiplicative inverses.
-
Q: Can I use a calculator to solve fraction division problems? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for developing mathematical fluency.
Conclusion: Mastering Fraction Division
Mastering fraction division is a significant step towards building a strong foundation in mathematics. By understanding the "Keep, Change, Flip" method, visualizing the process, and grasping the underlying mathematical principles, you can confidently tackle any fraction division problem. Remember to always simplify your answers and practice regularly to build your skills. The ability to divide fractions efficiently will not only improve your mathematical abilities but also broaden your ability to solve real-world problems across diverse fields. So, embrace the challenge, practice consistently, and watch your confidence in mathematics soar!
Latest Posts
Latest Posts
-
30 Percent Of What Number Is 12
Sep 20, 2025
-
Half Of 1 1 4 Inches
Sep 20, 2025
-
Which Of The Following Is Not A Proportion
Sep 20, 2025
-
How Many Bushels Of Apples Per Tree
Sep 20, 2025
-
How Many Hours Is 100000 Minutes
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 1/8 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.