3/4 + 3/4 Is How Much
faraar
Sep 20, 2025 · 7 min read
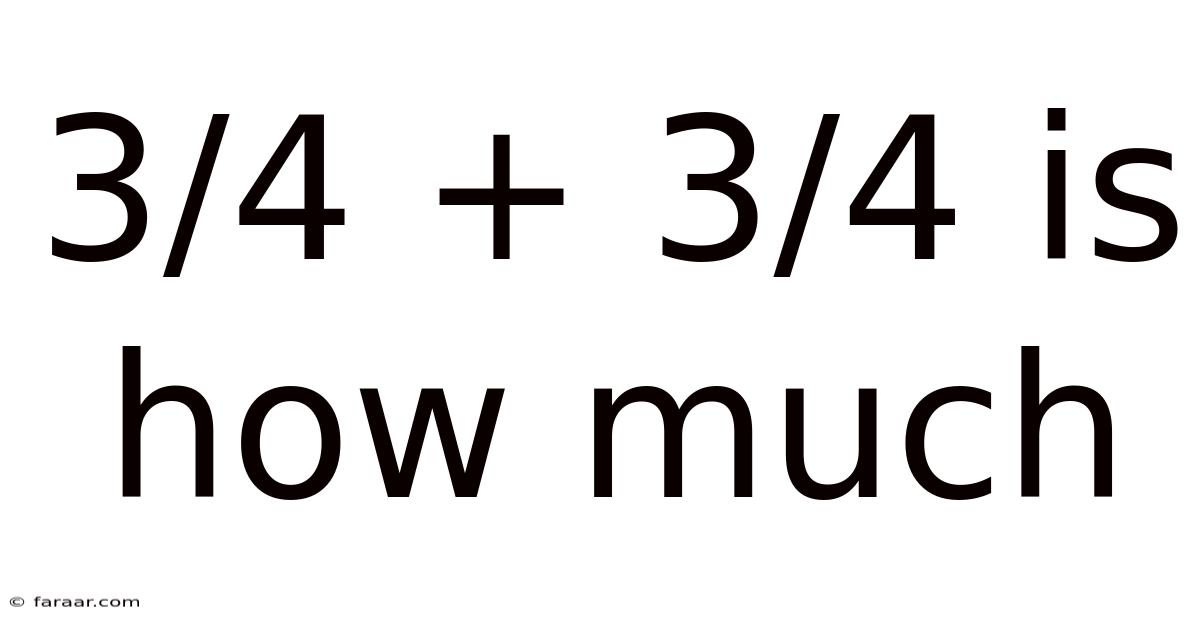
Table of Contents
3/4 + 3/4: A Deep Dive into Fraction Addition and its Applications
This article explores the seemingly simple addition problem: 3/4 + 3/4. While the answer might seem obvious to some, this seemingly straightforward calculation provides a fantastic opportunity to delve into the fundamental concepts of fraction addition, its practical applications, and some more advanced related topics. We will cover everything from the basic steps to visualizing fractions and exploring scenarios where this type of calculation is essential. Understanding fraction addition is crucial for various fields, from baking and construction to advanced mathematics and engineering.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 parts out of a total of 4 equal parts.
Adding Fractions: The Fundamental Rule
The key to adding fractions lies in having a common denominator. This means that the bottom numbers of the fractions must be the same before we can add the numerators. If the fractions already share a common denominator, as in our case (3/4 + 3/4), the process is straightforward:
- Add the numerators: Add the top numbers together. In our example, 3 + 3 = 6.
- Keep the denominator the same: The denominator remains unchanged. It stays as 4.
- Simplify the result (if necessary): The resulting fraction is 6/4. This fraction can be simplified. Since both the numerator (6) and the denominator (4) are divisible by 2, we can simplify it to 3/2 or 1 ½.
Therefore, 3/4 + 3/4 = 6/4 = 3/2 = 1 ½.
Visualizing Fraction Addition: A Practical Approach
Let's visualize this addition using a simple example. Imagine a pizza cut into four equal slices. The fraction 3/4 represents three slices of that pizza. Adding another 3/4 means adding three more slices. In total, you have six slices. Since the pizza was originally cut into four slices, you have 6/4 of the pizza, which simplifies to 1 ½ pizzas. This visual representation makes the concept of fraction addition more intuitive and easier to grasp.
Different Denominators: Expanding the Concept
While our example uses fractions with the same denominator, let's explore a scenario with different denominators. Suppose we want to add 1/2 + 1/4. Here's how we would proceed:
- Find the least common denominator (LCD): The LCD is the smallest number that both denominators (2 and 4) can divide into evenly. In this case, the LCD is 4.
- Convert the fractions to equivalent fractions with the LCD: We need to convert 1/2 to an equivalent fraction with a denominator of 4. To do this, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4.
- Add the fractions: Now that both fractions have the same denominator, we can add them: 2/4 + 1/4 = 3/4.
Therefore, 1/2 + 1/4 = 3/4.
Real-World Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require fractional measurements. Adding ingredients frequently involves adding fractions, ensuring the correct proportions. For instance, a recipe might call for 1/2 cup of sugar and 1/4 cup of flour. Knowing how to add 1/2 + 1/4 is crucial for accurate baking.
-
Construction and Engineering: Precision is paramount in construction and engineering. Measurements are often expressed in fractions of an inch or meter. Adding fractional dimensions is essential for accurate calculations and to ensure structural integrity. For example, a carpenter might need to add lengths of wood measured in fractions to determine the total length required for a project.
-
Finance: Dealing with percentages and proportions often necessitates fraction addition. For instance, calculating the total percentage increase or decrease across multiple financial periods often involves working with fractions.
-
Data Analysis: In data analysis, dealing with proportions and ratios is common. This often involves working with fractions and the ability to add them accurately is fundamental.
Mixed Numbers and Improper Fractions
Our example, 3/4 + 3/4, resulted in an improper fraction (6/4), where the numerator is larger than the denominator. Improper fractions can be converted to mixed numbers, which consist of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator).
To convert 6/4 to a mixed number:
- Divide the numerator by the denominator: 6 ÷ 4 = 1 with a remainder of 2.
- The whole number is the quotient: The whole number is 1.
- The fraction is the remainder over the denominator: The fraction is 2/4, which simplifies to 1/2.
Therefore, 6/4 = 1 ½.
Adding More Than Two Fractions
The principles of fraction addition extend to adding more than two fractions. The process remains the same: find the least common denominator, convert the fractions to equivalent fractions with the LCD, and then add the numerators. For instance:
1/2 + 1/4 + 1/8
- Find the LCD: The LCD of 2, 4, and 8 is 8.
- Convert to equivalent fractions: 1/2 = 4/8, 1/4 = 2/8.
- Add the fractions: 4/8 + 2/8 + 1/8 = 7/8
Therefore, 1/2 + 1/4 + 1/8 = 7/8.
Subtraction of Fractions: A Related Concept
Subtracting fractions follows a similar process to addition. The key is to ensure a common denominator before subtracting the numerators. For example, to subtract 1/4 from 3/4:
3/4 - 1/4 = (3-1)/4 = 2/4 = 1/2
Frequently Asked Questions (FAQs)
Q: What if the fractions have different denominators and finding the LCD is challenging?
A: For more complex fractions, using prime factorization to find the LCD can be helpful. Prime factorization breaks down a number into its prime factors (numbers divisible only by 1 and themselves). Find the prime factors of each denominator, and the LCD will be the product of the highest powers of each prime factor present in the denominators.
Q: Can I add fractions with different denominators without finding the LCD?
A: While you can add fractions without explicitly finding the LCD, the process becomes more complex and involves multiplication of the numerators and denominators of both fractions. Finding the LCD simplifies the process significantly.
Q: Are there any shortcuts for adding fractions?
A: Some shortcuts exist, particularly for simple fractions, but understanding the fundamental principles of finding a common denominator is crucial for mastering fraction addition and subtraction.
Q: What happens if I try to add fractions and get a result that is larger than 1?
A: That’s perfectly fine. This simply means you have an improper fraction, which can be converted to a mixed number to better represent the result.
Conclusion: Mastering Fraction Addition for a Brighter Future
Mastering fraction addition is a cornerstone of mathematical understanding, with significant implications for various aspects of life. From everyday tasks like cooking and baking to more complex applications in engineering and finance, the ability to accurately add fractions is invaluable. By understanding the fundamental principles, visualizing fractions, and practicing regularly, you'll build a strong foundation in mathematics and equip yourself with the skills needed to tackle more advanced concepts with confidence. Remember, the seemingly simple calculation 3/4 + 3/4 = 1 ½ opens a door to a vast world of mathematical possibilities. Embrace the challenge, and you'll find the rewards well worth the effort.
Latest Posts
Latest Posts
-
Explain The Differences Between Expressions And Equations
Sep 20, 2025
-
The Spine Is Blank To The Heart
Sep 20, 2025
-
Can You Use Calculator On Teas Test
Sep 20, 2025
-
How Do You Find A Missing Angle Of A Triangle
Sep 20, 2025
-
Write A Rule For Each Transformation
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3/4 + 3/4 Is How Much . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.