3 1/4 Divided By 3 As A Fraction
faraar
Sep 10, 2025 · 5 min read
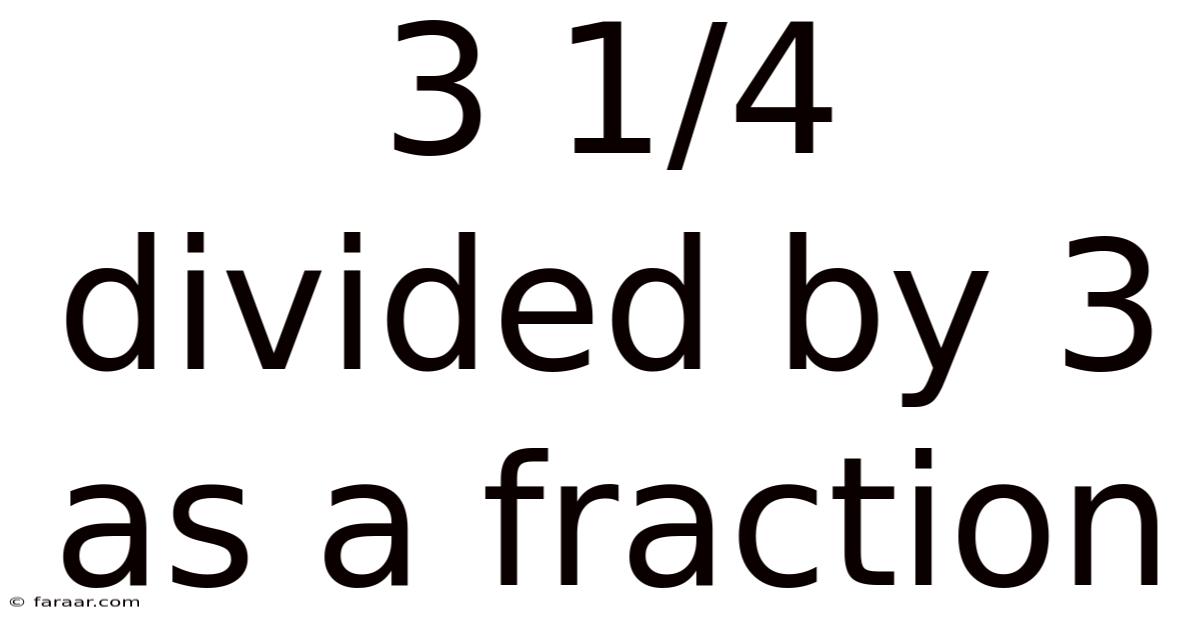
Table of Contents
Diving Deep into Fractions: Solving 3 1/4 Divided by 3
Dividing fractions can seem daunting, especially when mixed numbers are involved. This article will guide you through the process of solving 3 1/4 divided by 3, explaining each step clearly and providing a deeper understanding of the underlying mathematical principles. We'll cover various methods, address common misconceptions, and even explore the practical applications of such calculations. By the end, you'll not only know the answer but also possess a confident grasp of fraction division.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the division problem, let's solidify our understanding of mixed numbers and improper fractions. A mixed number, like 3 1/4, combines a whole number (3) and a fraction (1/4). An improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). To solve division problems involving mixed numbers, converting them to improper fractions is often the easiest approach.
To convert 3 1/4 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 3 x 4 = 12
- Add the numerator to the result: 12 + 1 = 13
- Keep the same denominator: The denominator remains 4.
Therefore, 3 1/4 is equivalent to the improper fraction 13/4.
Method 1: Converting to Improper Fractions and then Dividing
This is the most common and straightforward method for dividing mixed numbers. We've already converted 3 1/4 to 13/4. Now, let's divide it by 3. Remember that dividing by a whole number is the same as multiplying by its reciprocal. The reciprocal of 3 (or 3/1) is 1/3.
So, our problem becomes:
13/4 ÷ 3/1 = 13/4 x 1/3
To multiply fractions, we multiply the numerators together and the denominators together:
(13 x 1) / (4 x 3) = 13/12
This is an improper fraction. To convert it back to a mixed number:
- Divide the numerator by the denominator: 13 ÷ 12 = 1 with a remainder of 1
- The quotient becomes the whole number: 1
- The remainder becomes the numerator, and the denominator stays the same: 1/12
Therefore, 13/12 is equal to 1 1/12.
Thus, 3 1/4 divided by 3 equals 1 1/12.
Method 2: Dividing Directly Using Long Division (with Fractions)
While converting to improper fractions is generally preferred, it's helpful to understand how to approach division directly. This method might be less efficient but helps solidify the conceptual understanding of fraction division.
We can represent 3 1/4 ÷ 3 as:
(3 + 1/4) ÷ 3
This can be rewritten as:
(3 ÷ 3) + (1/4 ÷ 3)
Now we solve each part separately:
- 3 ÷ 3 = 1
- 1/4 ÷ 3 = 1/4 x 1/3 = 1/12
Combining the results:
1 + 1/12 = 1 1/12
Again, we arrive at the same answer: 1 1/12
The Importance of Understanding Reciprocals
The concept of reciprocals is crucial in fraction division. A reciprocal is simply a fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5 is 1/5. When dividing fractions, we change the division sign to a multiplication sign and use the reciprocal of the second fraction (the divisor). This is the fundamental principle behind converting a division problem into a multiplication problem, simplifying the calculation.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect answers when dividing fractions:
- Forgetting to convert mixed numbers to improper fractions: This is the most frequent error. Always convert mixed numbers to improper fractions before performing division.
- Incorrectly finding the reciprocal: Make sure you are flipping the correct fraction—the divisor, not the dividend.
- Errors in multiplication: Carefully multiply the numerators and denominators. Double-check your calculations to avoid simple arithmetic mistakes.
- Failing to simplify the answer: Always simplify the resulting fraction to its lowest terms.
Real-World Applications of Fraction Division
Understanding fraction division has numerous practical applications:
- Cooking and Baking: Dividing recipes to accommodate fewer servings often involves fraction division.
- Sewing and Crafting: Calculating fabric requirements or dividing yarn for a project requires precise fraction division.
- Construction and Engineering: Dividing measurements and materials accurately is critical in these fields.
- Data Analysis: Dividing proportions or percentages frequently involves fraction division.
Further Exploration: Dividing Fractions with Larger Numbers and More Complex Fractions
The principles discussed here apply to more complex scenarios. For instance, dividing larger mixed numbers or fractions with larger numerators and denominators involves the same steps: converting to improper fractions, taking the reciprocal of the divisor, multiplying the fractions, and simplifying the result. The process remains consistent, albeit potentially more computationally intensive.
Frequently Asked Questions (FAQ)
-
Q: Can I divide a mixed number by a whole number without converting to an improper fraction? A: While technically possible using the method of separating the whole number and fraction parts and dividing each separately (as demonstrated in Method 2), it's generally more efficient and less error-prone to convert to an improper fraction first.
-
Q: What if the result is an improper fraction? A: Convert the improper fraction back to a mixed number for a clearer and more easily understood answer.
-
Q: How do I simplify fractions? A: Simplify a fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For example, to simplify 12/18, the GCD is 6, so we divide both numerator and denominator by 6, resulting in 2/3.
-
Q: Are there other methods to divide fractions? A: While the methods described here are the most common and generally the easiest to understand, other less frequently used methods exist, primarily variations on converting to improper fractions or using long division with fractions.
Conclusion
Dividing fractions, particularly those involving mixed numbers, might initially appear challenging. However, by understanding the fundamental principles of converting mixed numbers to improper fractions, utilizing reciprocals, and performing multiplication, the process becomes significantly more manageable. Remember to always check your work for errors and simplify your answer to its lowest terms. Mastering fraction division is a valuable skill with wide-ranging applications in various aspects of life, from everyday tasks to more complex calculations. With practice and a clear understanding of the underlying concepts, you can confidently tackle any fraction division problem that comes your way.
Latest Posts
Latest Posts
-
Product Of Roots In A Quadratic Equation
Sep 10, 2025
-
The Buildup Of Electric Charges On An Object Is Called
Sep 10, 2025
-
How To Find Rel Max And Min
Sep 10, 2025
-
Can My Common App Essay Be More Than 650 Words
Sep 10, 2025
-
Simplify An Expression For The Perimeter Of The Rectangle
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 1/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.