3 1 2 2 2 3
faraar
Sep 12, 2025 · 6 min read
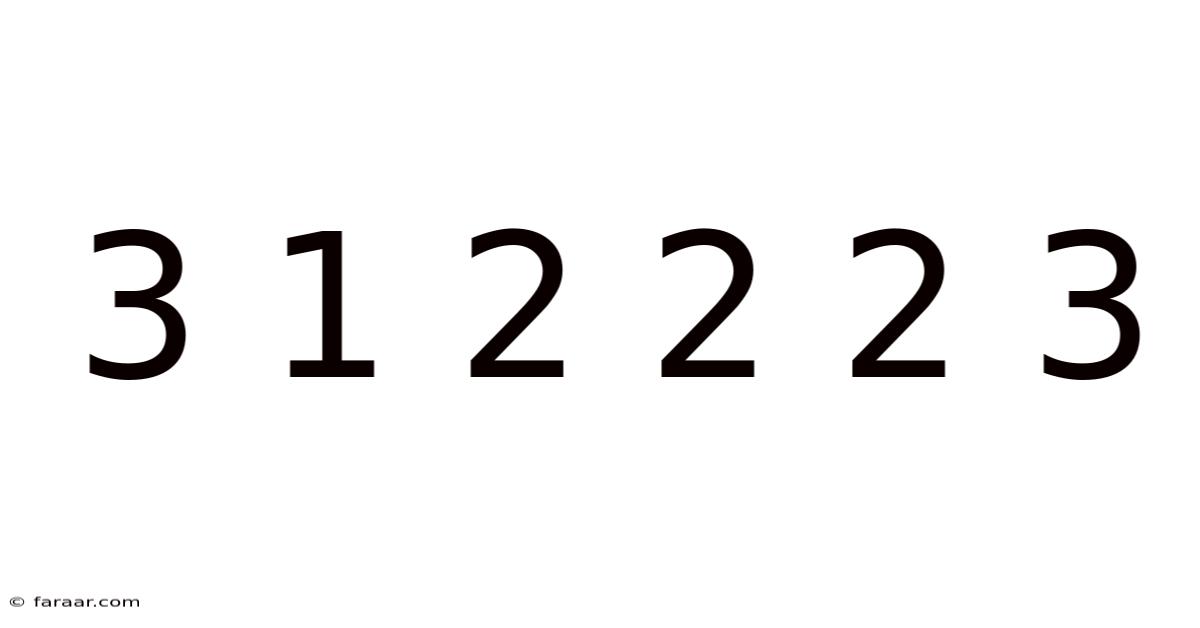
Table of Contents
Decoding the Seemingly Random Sequence: 3 1 2 2 2 3 – A Deep Dive into Patterns, Possibilities, and Problem-Solving
The sequence "3 1 2 2 2 3" might appear at first glance to be a random collection of numbers. However, the beauty of mathematics lies in its ability to unveil hidden patterns and structures even within seemingly chaotic arrangements. This seemingly simple sequence opens a door to exploring various mathematical concepts, problem-solving strategies, and the power of pattern recognition. This article will delve into different interpretations, possibilities, and underlying principles related to this numerical sequence. We will explore potential patterns, examine possible mathematical interpretations, and discuss how such sequences are analyzed in various fields.
I. Initial Observations and Potential Patterns
Before diving into complex analysis, let's start with simple observations. The sequence 3 1 2 2 2 3 exhibits several intriguing features:
-
Symmetry: The sequence is palindromic, meaning it reads the same forwards and backward. This inherent symmetry hints at a potentially underlying structure or rule governing its construction.
-
Repetition: The number 2 is repeated three times, forming a distinct cluster in the middle of the sequence. This repetition suggests a potential emphasis or significance placed on the number 2 within the sequence's structure.
-
Numerical Range: The numbers used are relatively small, ranging from 1 to 3. This limited range might suggest a simpler underlying rule compared to sequences with a wider numerical distribution.
These initial observations lay the groundwork for exploring potential mathematical interpretations and generating hypotheses about the sequence's origin.
II. Exploring Possible Interpretations
The apparent simplicity of the sequence "3 1 2 2 2 3" allows for multiple interpretations, depending on the assumed underlying generating process. Here are a few possibilities:
-
A Simple Arithmetic Sequence (Highly Unlikely): While it's unlikely, one could try to force-fit an arithmetic progression. However, the lack of a consistent common difference between consecutive terms rules out this interpretation.
-
A Recursive Sequence (Possible, but requires further definition): A recursive sequence defines each term based on preceding terms. However, without defining a specific recursive rule, there are infinitely many recursive sequences that could generate "3 1 2 2 2 3." We would need more terms in the sequence to infer a reliable recursive rule.
-
A Combinatorial Interpretation (Possible): Imagine a scenario involving choices or arrangements. For instance, consider a system with three distinct states (represented by 3), followed by a transition to a single state (1), then a series of transitions to a second state (2, repeated three times), and finally, a return to the initial state (3). This is just one possible narrative. Without more context, numerous combinatorial interpretations are feasible.
-
A Coding or Encryption Scheme (Possible): It's possible the sequence is part of a larger code or cipher. The simplicity might be a deceptive camouflage, hiding a more intricate underlying message. Further analysis would require additional data or context.
III. Expanding the Sequence: The Importance of More Data
The limited length of the sequence makes it difficult to definitively determine its generating rule. To unlock a more precise understanding, we need more data. If the sequence continues, it could reveal patterns that are not apparent in the current six-term sequence.
For instance, imagine the sequence extends: 3 1 2 2 2 3 1 2 2 2 3... This would strongly suggest a repeating pattern, simplifying the analysis considerably. Conversely, a different continuation, such as 3 1 2 2 2 3 4 5 6..., would imply a completely different generating mechanism.
The addition of even a few more terms would significantly enhance our ability to identify the underlying structure. This highlights the importance of data in mathematical and scientific investigations.
IV. Mathematical Concepts and Tools for Sequence Analysis
Analyzing numerical sequences often involves several mathematical tools and concepts:
-
Difference Tables: This method calculates the differences between consecutive terms, then the differences between those differences, and so on. Consistent patterns in the difference tables can reveal underlying polynomial relationships. However, in this case, the limited length of the sequence makes this analysis inconclusive.
-
Generating Functions: Generating functions provide a powerful way to represent sequences using formal power series. While suitable for more extended sequences, applying this technique to a sequence of only six terms is not very effective.
-
Statistical Analysis: If we suspect the sequence is random or has a stochastic component, statistical methods could be used to evaluate properties like autocorrelation or spectral density. However, the short sequence length limits the reliability of statistical inferences.
-
Pattern Recognition and Intuition: Often, the most powerful tool in sequence analysis is human intuition and pattern recognition. By carefully examining the sequence, looking for symmetries, repetitions, and potential relationships between terms, we can often develop insightful hypotheses about its origin.
V. Applications and Real-World Examples
Sequences of numbers appear extensively in various fields, including:
-
Computer Science: Sequences are used in algorithms, data structures, and coding. The analysis of sequences is crucial in understanding the efficiency and performance of algorithms.
-
Physics: Many physical phenomena are described by sequences of measurements or data points. Analyzing these sequences can reveal underlying physical laws and patterns.
-
Biology: Sequences of DNA, RNA, and proteins are fundamental to understanding biological processes. Analyzing these sequences is vital for genomics, proteomics, and other biological research areas.
-
Finance: Time series data in finance, such as stock prices, often exhibits patterns and trends that can be analyzed using sequence analysis techniques.
-
Cryptography: Sequences are central to many encryption and decryption methods. Understanding the underlying patterns in sequences is crucial for developing secure cryptographic systems.
The ability to analyze and understand numerical sequences is a fundamental skill across numerous disciplines.
VI. Conclusion: The Importance of Context and Further Investigation
The seemingly simple sequence "3 1 2 2 2 3" offers a valuable lesson in mathematical exploration. While we can propose various interpretations and hypotheses, the limited data prevents definitive conclusions. The true nature of the sequence can only be fully understood with additional information or context about its origin.
The exercise of attempting to decipher this sequence highlights the importance of:
-
Data Collection: The need for sufficient data to draw meaningful conclusions.
-
Pattern Recognition: The role of observation and intuition in identifying underlying structures.
-
Multiple Perspectives: The possibility of multiple interpretations and the need to consider various approaches.
-
Critical Thinking: The importance of evaluating the strength and limitations of different analytical methods.
This seemingly simple problem provides a rich opportunity to explore fundamental concepts in mathematics, problem-solving, and the scientific method. The quest to understand the sequence "3 1 2 2 2 3" serves as a reminder that even simple-looking problems can lead to deep insights and valuable learning experiences. Further investigation, incorporating additional data points or the source of the sequence, would undoubtedly illuminate its underlying nature. This exercise underscores the fundamental principle that exploration and a methodical approach are crucial for solving mathematical puzzles and gaining a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
Which Of The Statements Describes A Chemical Property
Sep 12, 2025
-
What Does 5 Milligrams Look Like
Sep 12, 2025
-
A Six Sided Number Cube Is Rolled Twice
Sep 12, 2025
-
Why Does Okonkwo Kill The Messenger
Sep 12, 2025
-
Which Of The Orbital Electron Configurations Is Not Possible
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 1 2 2 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.