2x Y 8 In Slope Intercept Form
faraar
Sep 07, 2025 · 6 min read
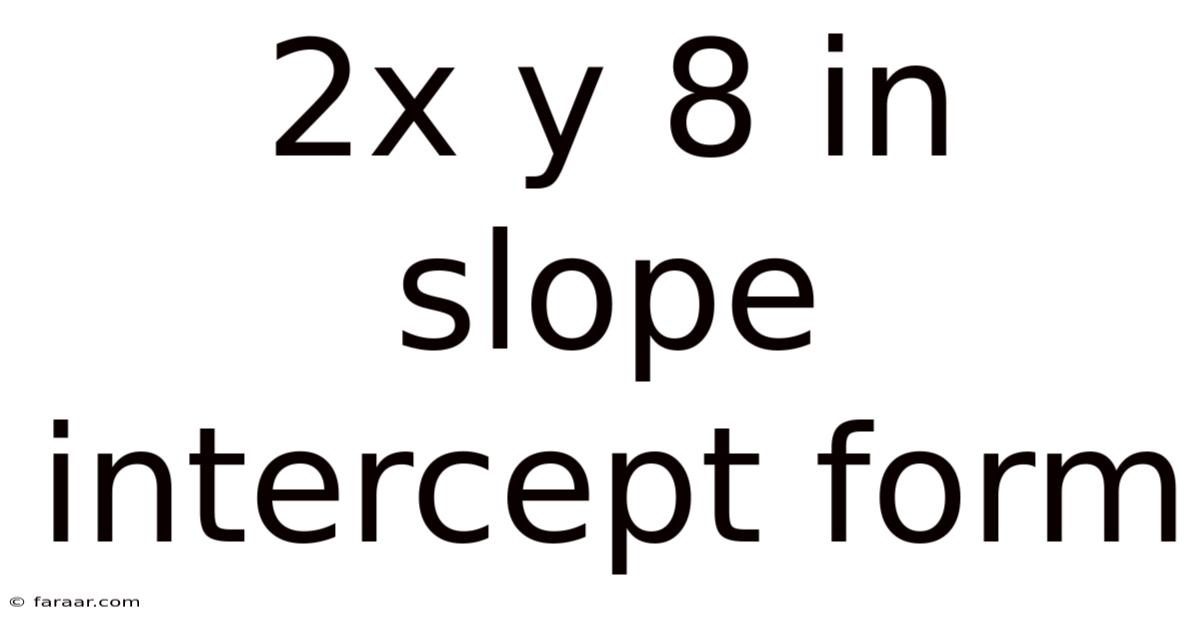
Table of Contents
Understanding and Applying the Slope-Intercept Form: 2x + y = 8
The equation 2x + y = 8 represents a linear relationship between two variables, x and y. Understanding how to convert this equation into slope-intercept form, y = mx + b, is crucial for visualizing the line on a graph and for solving various algebraic problems. This article will guide you through the process, explaining the significance of the slope (m) and y-intercept (b), and offering practical applications and examples. We will also delve into more advanced concepts to provide a comprehensive understanding of this fundamental algebraic concept.
From Standard Form to Slope-Intercept Form: A Step-by-Step Guide
The given equation, 2x + y = 8, is in standard form (Ax + By = C). To convert it to slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept, we need to isolate 'y'. Let's break down the process:
Step 1: Isolate the y term
Our goal is to get 'y' by itself on one side of the equation. To do this, we subtract 2x from both sides of the equation:
2x + y - 2x = 8 - 2x
This simplifies to:
y = -2x + 8
Step 2: Identify the slope (m) and y-intercept (b)
Now that the equation is in the form y = mx + b, we can easily identify the slope and y-intercept:
-
m (slope) = -2: The slope indicates the steepness and direction of the line. A negative slope means the line is decreasing (going downwards) from left to right. For every 1 unit increase in x, y decreases by 2 units.
-
b (y-intercept) = 8: The y-intercept is the point where the line crosses the y-axis (where x = 0). In this case, the line crosses the y-axis at the point (0, 8).
Visualizing the Line: Graphing the Equation
Now that we have the slope and y-intercept, we can easily graph the line.
-
Plot the y-intercept: Start by plotting the point (0, 8) on the y-axis.
-
Use the slope to find another point: The slope is -2, which can be expressed as -2/1. This means that for every 1 unit increase in x, y decreases by 2 units. Starting from (0, 8), move 1 unit to the right and 2 units down. This brings us to the point (1, 6).
-
Draw the line: Draw a straight line through the points (0, 8) and (1, 6). This line represents the equation y = -2x + 8.
Understanding the Slope and Y-Intercept: Deeper Insights
The slope and y-intercept provide crucial information about the linear relationship:
-
Slope (m): As mentioned earlier, the slope represents the rate of change of y with respect to x. A steeper slope indicates a faster rate of change. A positive slope indicates a positive correlation (as x increases, y increases), while a negative slope indicates a negative correlation (as x increases, y decreases). A slope of zero indicates a horizontal line (no change in y as x changes). An undefined slope indicates a vertical line (infinite change in y for a small change in x).
-
Y-intercept (b): The y-intercept represents the value of y when x is zero. It's the starting point of the line on the y-axis. In real-world applications, the y-intercept often represents an initial value or a base amount.
Real-World Applications: Putting it into Practice
Linear equations, like y = -2x + 8, are used to model numerous real-world scenarios. Here are a few examples:
-
Cost Analysis: Imagine a company that charges a fixed fee of $8 plus $2 per unit produced. The equation y = -2x + 8 could represent the relationship between the number of units produced (x) and the total cost (y), assuming a negative cost is a refund of some sort. Though unrealistic, this demonstrates the concept.
-
Temperature Conversion: Temperature conversion between Celsius and Fahrenheit can be represented by a linear equation. The slope and y-intercept would be specific constants derived from the conversion formula.
-
Distance-Time Relationships: The distance traveled by an object at a constant speed can be modeled using a linear equation. The slope would represent the speed, and the y-intercept would represent the initial distance.
Advanced Concepts and Extensions
Let's explore some related concepts that build upon the understanding of slope-intercept form:
-
Finding the x-intercept: The x-intercept is the point where the line crosses the x-axis (where y = 0). To find the x-intercept for y = -2x + 8, set y = 0 and solve for x:
0 = -2x + 8 2x = 8 x = 4
The x-intercept is (4, 0).
-
Parallel and Perpendicular Lines: Two lines are parallel if they have the same slope. Two lines are perpendicular if the product of their slopes is -1. For example, a line parallel to y = -2x + 8 would have a slope of -2, while a line perpendicular to y = -2x + 8 would have a slope of 1/2.
-
Systems of Linear Equations: Solving systems of linear equations involves finding the point where two or more lines intersect. This can be done graphically or algebraically using methods like substitution or elimination.
-
Linear Inequalities: Instead of an equation, we might have an inequality, such as y > -2x + 8. This represents the region above the line y = -2x + 8.
Frequently Asked Questions (FAQ)
-
Q: What if the equation isn't in standard form?
A: If the equation is not in standard form, you'll need to manipulate it algebraically to isolate 'y' and get it into the slope-intercept form (y = mx + b).
-
Q: What does a slope of zero mean?
A: A slope of zero means the line is horizontal. The y-value remains constant regardless of the x-value.
-
Q: What does an undefined slope mean?
A: An undefined slope means the line is vertical. The x-value remains constant regardless of the y-value.
-
Q: How can I determine if two lines are parallel or perpendicular?
A: Compare their slopes. Parallel lines have the same slope. Perpendicular lines have slopes that are negative reciprocals of each other (their product is -1).
Conclusion: Mastering the Slope-Intercept Form
Converting the equation 2x + y = 8 into slope-intercept form (y = -2x + 8) allows us to easily visualize the line, understand its properties (slope and y-intercept), and apply it to various real-world problems. By grasping the fundamental concepts of slope and y-intercept, and by exploring the advanced topics discussed, you'll build a strong foundation in linear algebra. Remember to practice regularly to solidify your understanding and apply these concepts effectively in different contexts. The more you work with linear equations, the more intuitive the relationships between slope, y-intercept, and graphical representation will become. This fundamental understanding is key to progressing to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
What Is The Difference Between Experimental And Theoretical Probability
Sep 07, 2025
-
Gaining Or Losing Electrons Is Called
Sep 07, 2025
-
Find The Value Of X Y And Z
Sep 07, 2025
-
Find The Equation Of The Line Below
Sep 07, 2025
-
What Is The Most Abundant Isotope For Calcium
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 2x Y 8 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.