2x Y 8 3x 5y 25
faraar
Sep 18, 2025 · 5 min read
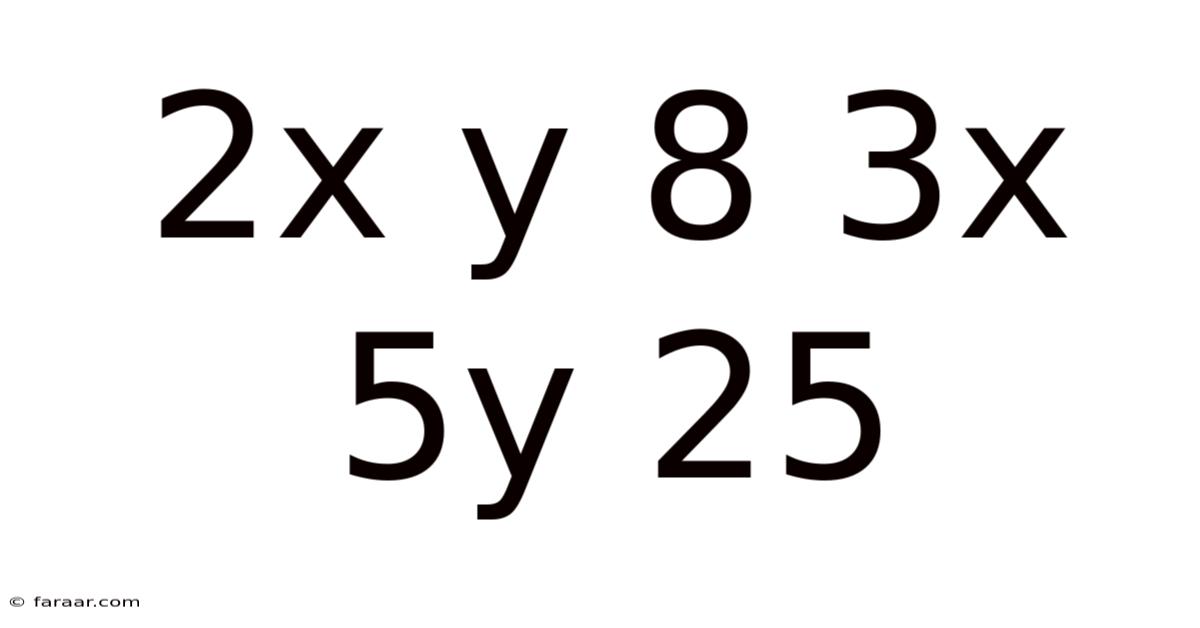
Table of Contents
Unlocking the Secrets of Simultaneous Equations: Solving 2x + 8 = 3x + 5y = 25
This article delves into the fascinating world of simultaneous equations, specifically tackling the problem presented by the equations 2x + 8 = 3x + 5y = 25. We'll break down the solution step-by-step, explaining the underlying principles and providing a clear understanding of the methods involved. Understanding simultaneous equations is crucial in various fields, from basic algebra to advanced physics and economics. This comprehensive guide will not only solve this specific problem but also empower you to tackle similar equations with confidence.
Introduction: Understanding Simultaneous Equations
Simultaneous equations involve finding the values of two or more variables that satisfy all equations in a given system. In our case, we have a system seemingly containing three equations, but in reality, it represents two distinct equations connected through a shared variable:
- Equation 1: 2x + 8 = 3x + 5y
- Equation 2: 3x + 5y = 25
Notice that the expression '3x + 5y' acts as a bridge connecting the two equations. Solving this system requires us to use algebraic manipulation to eliminate one variable and solve for the other. There are several methods to achieve this, and we'll explore the most efficient approaches.
Method 1: Substitution
The substitution method involves solving one equation for one variable in terms of the other and then substituting this expression into the second equation. Let's start by simplifying Equation 1:
-
Simplify Equation 1: Subtracting 2x from both sides of Equation 1 gives us: 8 = x + 5y
-
Solve for x: Subtracting 5y from both sides results in: x = 8 - 5y
-
Substitute: Now we substitute the expression for x (8 - 5y) into Equation 2: 3(8 - 5y) + 5y = 25
-
Solve for y: Expanding and simplifying: 24 - 15y + 5y = 25 This simplifies to -10y = 1, therefore y = -1/10 or -0.1
-
Substitute back to find x: Substitute the value of y (-0.1) back into either Equation 1 or the simplified expression for x (x = 8 - 5y). Using the simplified expression: x = 8 - 5(-0.1) = 8 + 0.5 = 8.5
Therefore, the solution using the substitution method is x = 8.5 and y = -0.1.
Method 2: Elimination
The elimination method, also known as the addition or subtraction method, involves manipulating the equations to eliminate one variable by adding or subtracting them. While this method is typically used when both equations are in the standard form (Ax + By = C), we can adapt it here.
-
Rearrange Equation 1: Rewrite Equation 1 in the standard form: x + 5y = 8
-
Set up for Elimination: Now we have:
- x + 5y = 8
- 3x + 5y = 25
-
Eliminate y: Notice that both equations have a '5y' term. Subtracting the first equation from the second eliminates 'y': (3x + 5y) - (x + 5y) = 25 - 8
-
Solve for x: This simplifies to 2x = 17, therefore x = 17/2 = 8.5
-
Substitute to find y: Substitute the value of x (8.5) back into either of the original equations. Using the first equation (x + 5y = 8): 8.5 + 5y = 8
-
Solve for y: Solving for y gives us 5y = -0.5, therefore y = -0.1
Again, the solution using the elimination method is x = 8.5 and y = -0.1.
Verification of the Solution
It's crucial to verify our solution by substituting the values of x and y into both original equations:
-
Equation 1 (2x + 8 = 3x + 5y): 2(8.5) + 8 = 3(8.5) + 5(-0.1) => 17 + 8 = 25.5 - 0.5 => 25 = 25 (Correct!)
-
Equation 2 (3x + 5y = 25): 3(8.5) + 5(-0.1) = 25 => 25.5 - 0.5 = 25 => 25 = 25 (Correct!)
Both equations are satisfied, confirming the accuracy of our solution: x = 8.5 and y = -0.1.
Graphical Representation
Simultaneous equations can also be solved graphically. Each equation represents a straight line on a Cartesian plane. The point where these lines intersect represents the solution to the system of equations. In this case, the lines x + 5y = 8 and 3x + 5y = 25 would intersect at the point (8.5, -0.1). While graphing provides a visual representation, algebraic methods are generally more precise and efficient for finding the exact solution.
Further Exploration: Systems with No Solution or Infinite Solutions
It's important to note that not all systems of simultaneous equations have a unique solution. Some systems have no solution (parallel lines that never intersect) or infinitely many solutions (lines that coincide). These cases arise when the equations are dependent or inconsistent.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve simultaneous equations? A: Yes, many graphing calculators and online calculators can solve simultaneous equations. However, understanding the underlying methods is crucial for problem-solving and deeper comprehension.
-
Q: What if I have more than two equations with more than two variables? A: Solving systems with more than two variables requires more advanced techniques such as matrix methods (Gaussian elimination, Cramer's rule) or iterative methods.
-
Q: Are there other methods for solving simultaneous equations? A: Yes, methods like Cramer's rule, which uses determinants, are also used to solve simultaneous equations, particularly useful for larger systems.
-
Q: Why is it important to learn about simultaneous equations? A: Simultaneous equations are fundamental to many areas of mathematics, science, and engineering. They are used to model real-world problems involving multiple interacting variables and are essential for problem-solving in numerous fields.
Conclusion: Mastering Simultaneous Equations
Solving simultaneous equations, even seemingly complex ones like 2x + 8 = 3x + 5y = 25, becomes manageable with a systematic approach. Understanding both the substitution and elimination methods empowers you to tackle various types of simultaneous equation problems. By mastering these techniques, you'll not only be able to find solutions efficiently but also gain a deeper understanding of the fundamental principles underpinning this essential area of mathematics. Remember to always verify your solution and consider the graphical interpretation to solidify your understanding. The ability to solve simultaneous equations is a valuable skill applicable across various academic disciplines and professional fields.
Latest Posts
Latest Posts
-
How To Find Sides And Angles Of A Triangle
Sep 18, 2025
-
Bd Bisects Angle Abc Find The Value Of X
Sep 18, 2025
-
Is A Covalent Bond Between Two Nonmetals
Sep 18, 2025
-
What Is The Gcf Of 20 And 40
Sep 18, 2025
-
Examples Of Statistical And Nonstatistical Questions
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2x Y 8 3x 5y 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.