27 Is 6 Of What Number
faraar
Aug 29, 2025 · 5 min read
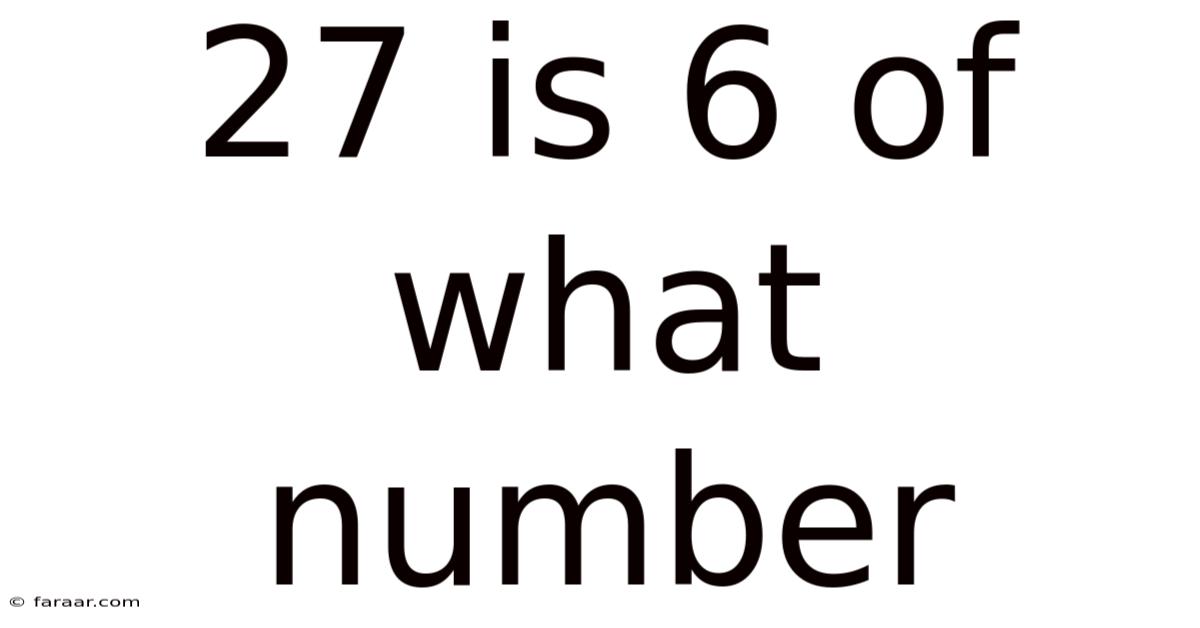
Table of Contents
27 is 6% of What Number? Unveiling the Power of Percentages
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing financial data and understanding statistical information. This article will delve into the question: "27 is 6% of what number?" We'll not only solve this specific problem but also explore the underlying principles of percentage calculations, offering various approaches to tackle similar problems and building a strong foundation in percentage-based problem-solving. This will help you confidently navigate percentage-related challenges in various contexts.
Understanding the Fundamentals of Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. Understanding this basic concept is key to solving percentage problems.
Solving "27 is 6% of What Number?"
Our central question asks us to find the whole number (the total) when we know a part of it (27) represents 6% of the total. We can approach this problem using several methods.
Method 1: Using the Proportion Method
This method relies on setting up a proportion, equating two ratios. We can represent the problem as follows:
- Part/Whole = Percentage/100
In our case:
- 27/x = 6/100
Where 'x' represents the unknown number we're trying to find. To solve for x, we can cross-multiply:
- 27 * 100 = 6 * x
- 2700 = 6x
- x = 2700 / 6
- x = 450
Therefore, 27 is 6% of 450.
Method 2: Using the Decimal Method
This method converts the percentage to a decimal and then sets up an equation. To convert 6% to a decimal, we divide by 100:
- 6% = 6/100 = 0.06
Now, we can express the problem as an equation:
- 0.06 * x = 27
To solve for x, we divide both sides by 0.06:
- x = 27 / 0.06
- x = 450
Again, we find that 27 is 6% of 450.
Method 3: Using the Formula Method
We can derive a general formula for solving these types of problems. If we let:
- P = the part (27 in our case)
- R = the percentage (6% or 0.06)
- W = the whole (the unknown number)
The formula becomes:
- P = R * W
To solve for W, we rearrange the formula:
- W = P / R
Substituting our values:
- W = 27 / 0.06
- W = 450
This confirms our previous results: 27 is 6% of 450.
Expanding Our Understanding: Variations and Applications
The fundamental principles we've applied can be extended to solve a variety of percentage problems. Let's explore some examples:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, what percentage of 80 is 20? The calculation would be (20/80) * 100 = 25%.
-
Finding the part: If you know the percentage and the whole, you can calculate the part. For example, what is 15% of 60? The calculation would be 0.15 * 60 = 9.
-
Real-world applications: Percentage calculations are crucial in many fields:
- Finance: Calculating interest, discounts, taxes, and profit margins.
- Statistics: Analyzing data, calculating probabilities, and understanding trends.
- Retail: Determining sale prices, markups, and discounts.
- Science: Expressing concentrations, errors, and changes in measurements.
Addressing Common Challenges and FAQs
Many students struggle with percentage problems due to a lack of understanding of the underlying concepts or difficulty in applying the correct formula. Here are some frequently asked questions and their answers:
Q: What if the percentage is greater than 100%?
A: A percentage greater than 100% indicates that the part is larger than the whole. This is perfectly valid in certain contexts. For example, if a company's sales this year are 120% of last year's sales, it means this year's sales exceeded last year's by 20%. The same methods discussed above apply, just remember that the resulting "whole" will be smaller than the "part."
Q: How do I handle percentages with decimals?
A: Treat decimal percentages the same way you treat whole number percentages. Simply convert the decimal percentage to a decimal fraction (e.g., 7.5% = 0.075) before applying the chosen method.
Q: How can I improve my accuracy in percentage calculations?
A: Practice is key! Solve a wide variety of percentage problems, starting with simple ones and gradually increasing the complexity. Pay close attention to the wording of the problem to ensure you're correctly identifying the part, the whole, and the percentage. Using a calculator can help avoid calculation errors, but understanding the underlying principles is essential.
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators are excellent tools for performing the arithmetic involved in percentage calculations, especially for more complex problems. However, understanding the underlying concepts is vital, as the calculator only performs the computations; it doesn't interpret the problem for you. You still need to set up the correct equation or proportion.
Q: What are some common mistakes to avoid?
A: Some common mistakes include:
- Confusing the part and the whole: Carefully read the problem to identify which value represents the part and which represents the whole.
- Incorrectly converting percentages to decimals: Remember to divide the percentage by 100 to convert it to a decimal.
- Arithmetic errors: Double-check your calculations to avoid simple mistakes.
- Not understanding the context: Always consider the real-world implications of the percentage to ensure your answer makes sense in the given scenario.
Conclusion: Mastering Percentages for a Brighter Future
The ability to confidently solve percentage problems is an invaluable skill with far-reaching applications. By mastering the different methods outlined in this article—the proportion method, the decimal method, and the formula method—you can tackle a wide range of percentage-based challenges. Remember to practice regularly, understand the underlying principles, and avoid common pitfalls. With dedication and practice, you'll build a strong foundation in percentage calculations, empowering you to succeed in various academic, professional, and personal endeavors. The solution to "27 is 6% of what number?" – 450 – is not just an answer; it's a stepping stone to a deeper understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
Graph The Equation Y 1 2x 2
Aug 29, 2025
-
What Is An Equivalent Fraction To 4 5
Aug 29, 2025
-
Common Multiples Of 9 And 10
Aug 29, 2025
-
Eliminate The Parameter To Find A Cartesian Equation
Aug 29, 2025
-
Sun And Moon Letters In Arabic
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about 27 Is 6 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.