25 Of What Number W Is 9
faraar
Sep 20, 2025 · 5 min read
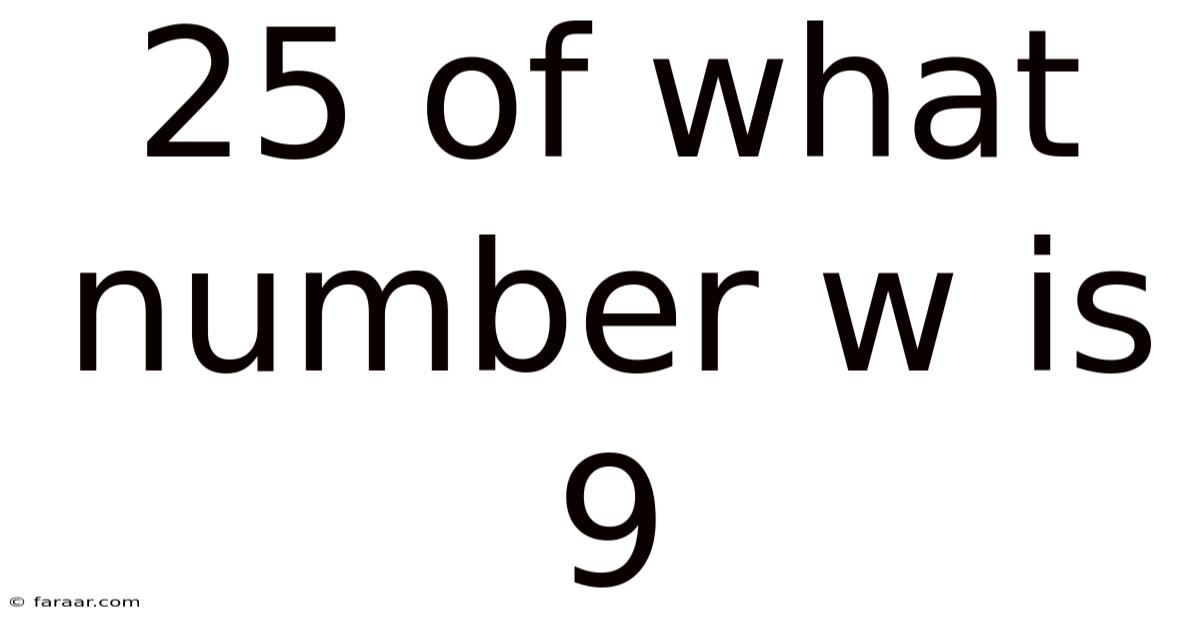
Table of Contents
Solving the Equation: 25% of What Number is 9? A Comprehensive Guide
This article explores the solution to the mathematical problem: "25% of what number is 9?". We'll break down the problem step-by-step, covering various approaches – from basic arithmetic to algebraic methods – ensuring a complete understanding, regardless of your mathematical background. We’ll also delve into the practical applications of percentage calculations and address frequently asked questions. This detailed explanation aims to not just provide the answer but to build a solid foundation in understanding percentages and their real-world relevance.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of one hundred." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Understanding this fundamental concept is crucial for solving percentage problems. Many everyday situations involve percentages, from calculating discounts and taxes to understanding interest rates and statistical data.
Method 1: Using the Basic Arithmetic Approach
The problem "25% of what number is 9?" can be translated into a mathematical equation. Let's represent the unknown number as 'x'. The equation becomes:
0.25 * x = 9
To solve for x, we need to isolate it on one side of the equation. We can do this by dividing both sides by 0.25:
x = 9 / 0.25
Calculating this gives us:
x = 36
Therefore, 25% of 36 is 9.
Method 2: Using Fractions
We can also approach this problem using fractions. Remember that 25% is equivalent to the fraction 25/100, which simplifies to 1/4. So, our equation becomes:
(1/4) * x = 9
To solve for x, we multiply both sides by 4:
x = 9 * 4
x = 36
This confirms our previous result: 25% of 36 is 9. This fractional method offers an alternative perspective and reinforces the understanding of percentage-to-fraction conversion.
Method 3: The Algebraic Approach
For those familiar with algebra, we can use a more formal approach. We start with the same equation:
0.25x = 9
We can solve this using algebraic manipulation. Dividing both sides by 0.25:
x = 9 / 0.25
x = 36
This algebraic method demonstrates a more structured and generalized approach to solving percentage problems, making it applicable to a wider range of complex equations.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives. Here are some examples:
-
Discounts and Sales: Stores often advertise discounts as percentages (e.g., "20% off"). Knowing how to calculate percentages allows you to determine the actual price reduction.
-
Taxes: Sales tax and income tax are calculated as percentages of the purchase price or income.
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest calculations is crucial for financial planning.
-
Statistics and Data Analysis: Percentages are frequently used to represent data in charts, graphs, and reports. Understanding percentages helps in interpreting statistical information effectively.
-
Tip Calculation: Calculating tips in restaurants often involves determining a percentage of the bill amount.
-
Grade Calculation: Many educational systems use percentages to represent grades and overall academic performance.
Expanding on Percentage Concepts: Proportions and Ratios
Understanding percentages is intrinsically linked to the concepts of proportions and ratios. A ratio is a comparison of two quantities, while a proportion is a statement that two ratios are equal. Percentage problems can be solved using proportions. For instance, the problem "25% of what number is 9?" can be set up as a proportion:
25/100 = 9/x
Cross-multiplying and solving for x:
25x = 900
x = 36
This method highlights the interconnectedness of percentages, ratios, and proportions, offering a versatile approach to solving percentage-related problems.
Beyond the Basics: Dealing with More Complex Percentage Problems
While the problem "25% of what number is 9?" is relatively straightforward, the same principles can be applied to more complex scenarios. For instance, consider a problem involving multiple percentages or finding the percentage increase or decrease between two values. These more complex problems require a thorough understanding of fundamental percentage concepts and often involve multiple steps. The key is to break down the problem into smaller, manageable parts, applying the basic principles of percentage calculations systematically.
Frequently Asked Questions (FAQ)
Q1: What if the percentage is not a whole number, like 12.5%?
A1: The same methods apply. You can convert 12.5% to a decimal (0.125) or a fraction (1/8) and proceed with the calculation as shown in the examples above.
Q2: Can I use a calculator for these types of problems?
A2: Absolutely! Calculators are helpful, especially for more complex percentage calculations. However, it's essential to understand the underlying principles to avoid making errors in inputting the data or interpreting the results.
Q3: Are there any online tools or resources to help me practice percentage problems?
A3: Many online educational websites and apps offer interactive exercises and quizzes on percentages. These resources can provide valuable practice and help reinforce your understanding.
Q4: How can I improve my understanding of percentages?
A4: Consistent practice with different types of percentage problems is key. Start with simpler problems and gradually work your way up to more complex ones. Understanding the underlying concepts of fractions, ratios, and proportions is crucial for mastering percentages.
Conclusion
Solving the equation "25% of what number is 9?" involves applying fundamental principles of percentage calculations. We've explored various approaches, from basic arithmetic and fractions to the more formal algebraic method. The solution, x = 36, highlights the simplicity and practicality of these methods. Remember, a solid understanding of percentages is essential for navigating various aspects of daily life, from personal finance to data analysis. By mastering these concepts and practicing regularly, you can confidently tackle a wide range of percentage problems and apply this knowledge to real-world situations. The key is to understand the underlying principles and to choose the method that best suits your mathematical comfort level and the complexity of the problem.
Latest Posts
Latest Posts
-
Find The Electronegativity Difference Between K And Cl
Sep 20, 2025
-
How Does The Syntax Contribute To The Voice
Sep 20, 2025
-
What Does A Que Hora Mean
Sep 20, 2025
-
How To Find The Specific Heat Of A Calorimeter
Sep 20, 2025
-
Where Is The Dna Found In The Prokaryotic Cell
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Of What Number W Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.