25 Of What Number Is 9
faraar
Sep 12, 2025 · 5 min read
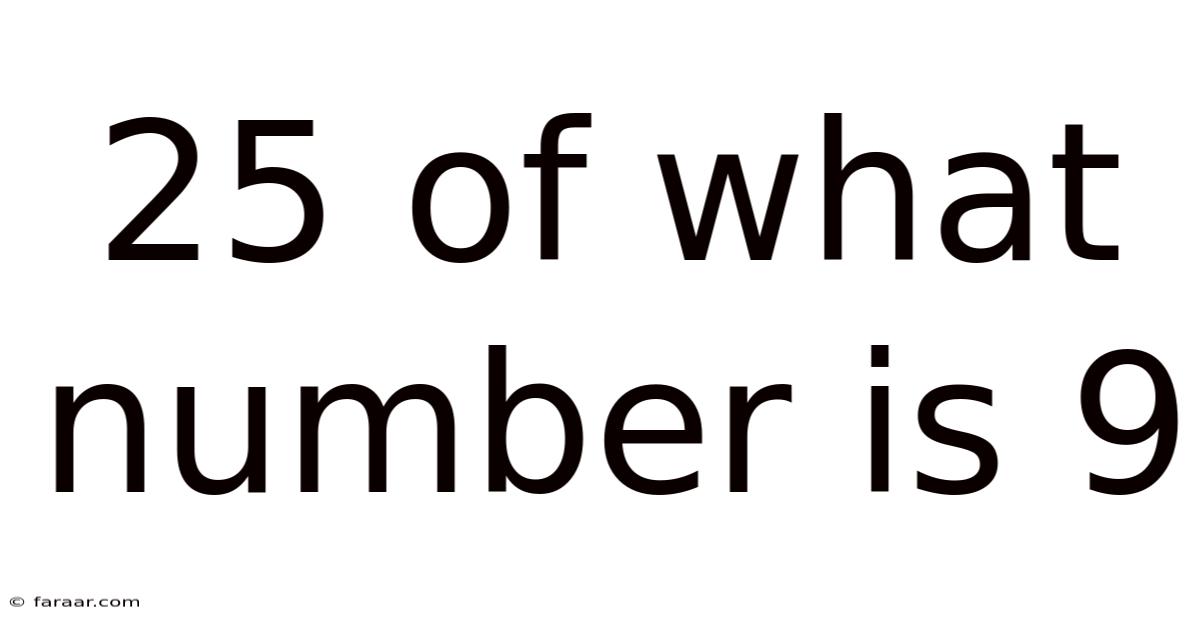
Table of Contents
25% of What Number is 9? Unlocking the World of Percentages
Finding 25% of a number is a fundamental concept in mathematics, crucial for various applications from calculating discounts to understanding financial statements. This article delves into the methods of solving the equation "25% of what number is 9?", exploring different approaches, explaining the underlying principles, and providing a comprehensive understanding of percentages. We'll go beyond simply finding the answer and explore the broader implications of percentage calculations.
Understanding the Problem: Deconstructing the Question
The question "25% of what number is 9?" essentially translates into a mathematical equation. We can represent this using algebraic notation:
0.25 * x = 9
Where:
- 0.25 represents 25% (expressed as a decimal – remember to convert percentages to decimals by dividing by 100).
- x is the unknown number we're trying to find.
- 9 is the result of 25% of x.
Solving this equation will give us the value of 'x', the number we are seeking.
Method 1: The Algebraic Approach
This is the most straightforward and mathematically rigorous method. We need to isolate 'x' in our equation:
0.25 * x = 9
To solve for x, we divide both sides of the equation by 0.25:
x = 9 / 0.25
x = 36
Therefore, 25% of 36 is 9.
Method 2: The Proportion Method
This method utilizes the concept of proportions. A percentage can be expressed as a ratio. 25% is equivalent to the ratio 25/100, which simplifies to 1/4. We can set up a proportion:
25/100 = 9/x
Cross-multiplying gives us:
25x = 900
Dividing both sides by 25:
x = 900 / 25
x = 36
Again, we find that x = 36.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Percentage/100) * Total = Part
In our case:
- Percentage = 25
- Total = x (the unknown)
- Part = 9
Substituting these values into the formula:
(25/100) * x = 9
Simplifying:
0.25 * x = 9
Solving for x (as shown in Method 1):
x = 36
This method reinforces the fundamental relationship between percentages, totals, and parts.
Method 4: Working Backwards from a Fraction
Since 25% is equivalent to ¼ (one-quarter), we can rephrase the question as:
"One-quarter of what number is 9?"
This implies that 9 represents one-quarter of the whole. To find the whole, we multiply 9 by 4 (the reciprocal of ¼):
9 * 4 = 36
This method provides an intuitive understanding of the problem, particularly helpful for those comfortable working with fractions.
Why Understanding Percentages is Crucial
The ability to solve percentage problems like "25% of what number is 9?" is a vital skill with broad applications across numerous fields:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentages. Understanding these calculations is essential for making informed financial decisions.
- Business: Analyzing sales data, market share, and profit/loss statements often relies heavily on percentage calculations.
- Science: Expressing experimental results, statistical data, and probabilities frequently involves percentages.
- Everyday Life: Calculating tips, understanding sale prices, and interpreting statistics in news reports all require a basic grasp of percentages.
Expanding Your Percentage Knowledge: Beyond the Basics
While solving "25% of what number is 9?" is a relatively straightforward problem, mastering percentages involves understanding several key concepts:
- Converting Percentages to Decimals and Fractions: Fluency in converting between percentages, decimals, and fractions is essential for efficient problem-solving. Remember, to convert a percentage to a decimal, divide by 100. To convert a decimal to a percentage, multiply by 100.
- Understanding Percentage Increase and Decrease: This involves calculating the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is similar, but the result will be negative.
- Calculating Percentage Points: A percentage point represents the absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
- Compounding Percentages: This refers to applying a percentage increase or decrease repeatedly over time. This is commonly used in financial calculations, such as compound interest.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Absolutely! Calculators can significantly speed up the process, especially for more complex percentage calculations. However, understanding the underlying methods is crucial for problem-solving and critical thinking.
-
Q: What if the percentage wasn't a whole number (e.g., 25.5%)? A: The methods described above still apply. Simply convert the percentage to its decimal equivalent (25.5% = 0.255) and proceed with the algebraic or proportion method.
-
Q: Are there other ways to solve this type of problem? A: Yes, there are other approaches, including using visual aids like pie charts or bar graphs to represent the problem and using iterative methods for approximate solutions. However, the methods described above are efficient and widely applicable.
Conclusion: Mastering the Power of Percentages
The ability to solve problems like "25% of what number is 9?" is more than just a mathematical skill; it’s a fundamental tool for navigating the world around us. By understanding the different methods for solving percentage problems and grasping the underlying principles, you empower yourself to confidently tackle real-world challenges involving percentages in finance, business, science, and everyday life. Remember that practice is key – the more you work with percentages, the more intuitive and comfortable you will become with these calculations. So, continue exploring, practicing, and expanding your understanding of this crucial mathematical concept. The world of percentages is vast and rewarding, offering endless opportunities for application and exploration.
Latest Posts
Latest Posts
-
Find The Equation Of A Horizontal Line
Sep 12, 2025
-
How Much Weight Can An Elevator Hold
Sep 12, 2025
-
Which Pair Does Not Have An Electric Force Between Them
Sep 12, 2025
-
How To Multiply Fractions With Polynomials
Sep 12, 2025
-
How To Find X In Angles
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 25 Of What Number Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.