20 Is 25 Percent Of What Number
faraar
Sep 10, 2025 · 5 min read
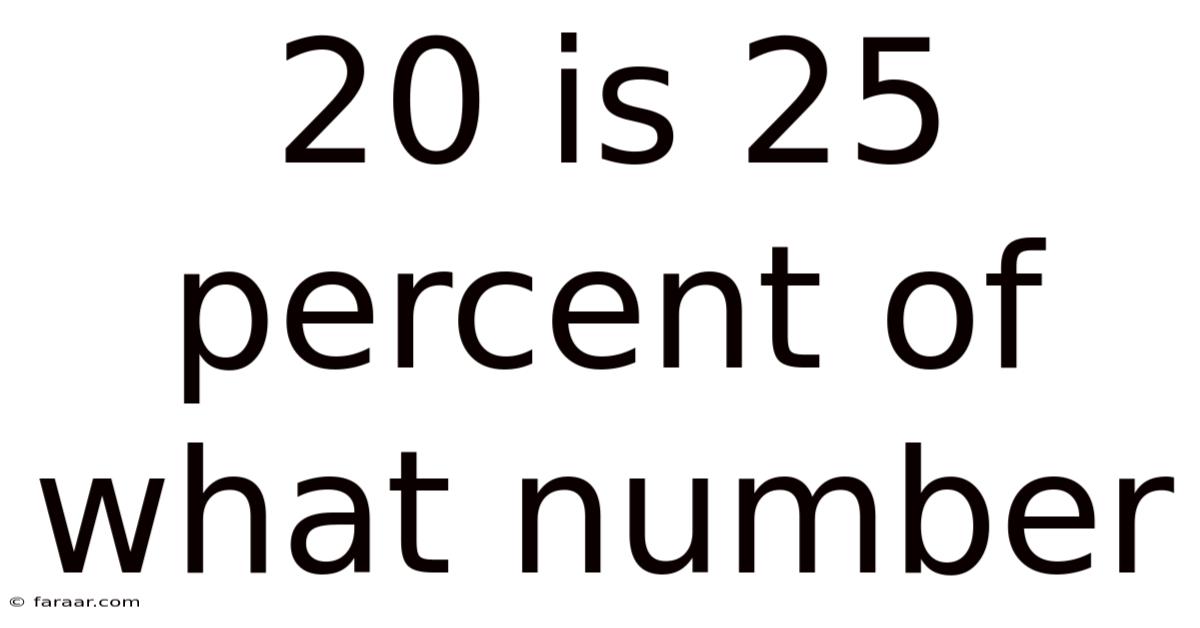
Table of Contents
20 is 25 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will guide you through the process of solving the problem "20 is 25 percent of what number," explaining the underlying principles, providing step-by-step solutions, and exploring various approaches to tackling similar percentage problems. We'll also delve into the practical applications of this type of calculation and address frequently asked questions.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. This fundamental understanding is crucial for solving percentage problems.
Method 1: Using the Proportion Method
The proportion method is a classic and intuitive approach to solving percentage problems. We set up a proportion, which is an equation stating that two ratios are equal. In this case, we know that 20 is 25% of an unknown number (let's call it 'x'). We can express this relationship as a proportion:
20/x = 25/100
To solve for x, we cross-multiply:
20 * 100 = 25 * x
2000 = 25x
Now, we isolate x by dividing both sides of the equation by 25:
x = 2000 / 25
x = 80
Therefore, 20 is 25% of 80.
Method 2: Using the Decimal Method
This method leverages the decimal equivalent of a percentage. We convert the percentage to a decimal by dividing it by 100. In this case, 25% becomes 0.25. The problem can then be expressed as an equation:
20 = 0.25 * x
To solve for x, we divide both sides of the equation by 0.25:
x = 20 / 0.25
x = 80
Again, we arrive at the solution: 20 is 25% of 80.
Method 3: Using the Formula Method
A more generalized formula for solving percentage problems is:
Part = Percentage * Whole
Where:
- Part represents the portion of the whole (in this case, 20).
- Percentage represents the percentage rate (in this case, 25%, or 0.25).
- Whole represents the total amount (the unknown value, x).
Substituting the known values into the formula:
20 = 0.25 * x
Solving for x as before:
x = 20 / 0.25
x = 80
This method reinforces the core concept and provides a framework for solving a wide variety of percentage problems.
Applying Percentage Calculations in Real-World Scenarios
The ability to calculate percentages is invaluable in various real-world situations. Here are a few examples:
-
Calculating Discounts: If a store offers a 25% discount on an item originally priced at $80, the discount amount is 0.25 * $80 = $20, resulting in a final price of $60. This calculation is the inverse of the problem we solved earlier.
-
Determining Tax Amounts: Understanding percentages helps calculate sales tax or value-added tax (VAT). If the sales tax is 6%, and the price of an item is $100, the tax amount is 0.06 * $100 = $6.
-
Analyzing Financial Statements: Financial reports often use percentages to express ratios and trends, such as profit margins, debt-to-equity ratios, and growth rates. Understanding percentage calculations allows for meaningful interpretation of these key financial metrics.
-
Understanding Statistics: Percentages are frequently used to represent statistical data, such as the percentage of a population with a certain characteristic or the success rate of a particular treatment.
-
Calculating Grades: Many grading systems are based on percentages. If a student scores 80 out of 100 on an exam, their grade is 80%.
These examples highlight the broad applicability of percentage calculations in daily life and professional contexts. Mastering these calculations empowers you to make informed decisions and understand complex information.
Solving Similar Percentage Problems
The methods described above can be adapted to solve any problem involving percentages. For instance, consider the following variations:
-
What is 15% of 60? Using the formula method: Part = 0.15 * 60 = 9.
-
30 is what percent of 150? Using the proportion method: 30/150 = x/100. Solving for x gives x = 20%, so 30 is 20% of 150.
-
45 is 75% of what number? Using the decimal method: 45 = 0.75 * x. Solving for x gives x = 60.
Frequently Asked Questions (FAQs)
Q1: What if the percentage is greater than 100%?
A1: Percentages greater than 100% represent values exceeding the whole. For example, if you invest $100 and your investment grows to $150, your return is 50% more than your initial investment, or a 150% increase relative to your initial investment.
Q2: How do I calculate percentages quickly without a calculator?
A2: For simple percentages, mental math tricks can be helpful. For example, 10% of a number is easily found by moving the decimal point one place to the left. 5% is half of 10%, and 25% is one-quarter of the number. Practice with these common percentages to build your mental calculation skills.
Q3: Are there any online tools or calculators for percentage calculations?
A3: Numerous online percentage calculators are available, providing a quick and easy way to perform these calculations.
Q4: Why is understanding percentages important?
A4: Understanding percentages is crucial for interpreting data, making financial decisions, understanding discounts and taxes, and navigating a wide variety of everyday situations. It's a fundamental skill applicable across many areas of life.
Q5: Can I use a different method besides the ones you've explained?
A5: Absolutely! While the methods explained are common and effective, other algebraic approaches can be employed to solve for the unknown variable (x). The key is to set up the problem correctly, reflecting the relationship between the given percentage, the known part, and the unknown whole.
Conclusion
Solving the problem "20 is 25 percent of what number?" demonstrates the fundamental principles of percentage calculations. By understanding the different methods – proportion, decimal, and formula – you can confidently approach various percentage problems. This skill is not only valuable for mathematical exercises but also essential for practical applications in finance, statistics, and everyday life. Remember, practice is key to mastering this essential mathematical concept. By consistently applying these methods, you'll develop a strong understanding of percentages and their widespread applications.
Latest Posts
Latest Posts
-
Find The Output Y When The Input X Is 4
Sep 10, 2025
-
How To Find Zeros In A Polynomial Function
Sep 10, 2025
-
Given 2 And 4 Are Vertical Angles
Sep 10, 2025
-
What Is 5 5 In Fraction Form
Sep 10, 2025
-
Each Pair Of Figures Is Similar Find The Missing Side
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 20 Is 25 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.