2 Tens 1 One X 10
faraar
Sep 22, 2025 · 6 min read
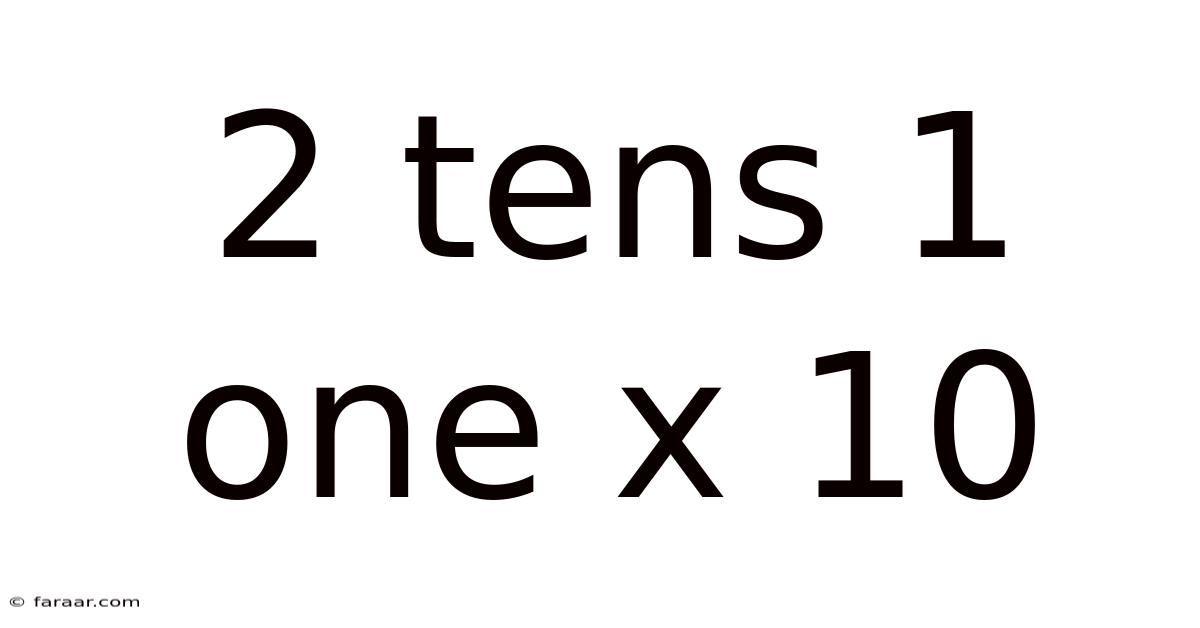
Table of Contents
Decoding "2 Tens 1 One x 10": A Deep Dive into Multiplication and Place Value
This article explores the seemingly simple mathematical expression "2 tens 1 one x 10," delving beyond the immediate answer to uncover the underlying principles of multiplication, place value, and their practical applications. We'll break down the problem step-by-step, examine the relevant mathematical concepts, and even explore how this fundamental calculation lays the groundwork for more complex mathematical operations. This understanding will be crucial for anyone seeking a strong foundation in arithmetic and a deeper grasp of numerical systems.
Understanding Place Value: The Foundation of Our Number System
Before tackling the multiplication, it's crucial to understand the concept of place value. Our number system is based on a decimal system, meaning it uses ten digits (0-9) and groups numbers in powers of ten. Each digit in a number holds a specific place value, representing its contribution to the overall value.
For example, in the number 21, the '2' represents two tens (20) and the '1' represents one one (1). This is often expressed as:
- 2 tens = 20
- 1 one = 1
Therefore, 2 tens 1 one is simply another way of representing the number 21. Understanding this representation is key to solving our problem efficiently.
Breaking Down the Multiplication: 2 Tens 1 One x 10
Now, let's address the multiplication: 2 tens 1 one x 10. We can approach this problem in several ways, each illuminating a different aspect of the mathematical principles involved.
Method 1: Direct Multiplication
The simplest approach is to convert "2 tens 1 one" into its numerical equivalent (21) and then perform the multiplication directly:
21 x 10 = 210
This is a straightforward calculation, easily performed using standard multiplication techniques. However, this method doesn't explicitly highlight the role of place value in the multiplication process.
Method 2: Distributive Property and Place Value
This method leverages the distributive property of multiplication, which states that a(b + c) = ab + ac. We can distribute the multiplication across the tens and ones place:
(2 tens + 1 one) x 10 = (20 + 1) x 10
Applying the distributive property:
(20 x 10) + (1 x 10) = 200 + 10 = 210
This approach demonstrates how the multiplication affects each place value separately. Multiplying the tens place (20) by 10 results in 200, and multiplying the ones place (1) by 10 results in 10. Adding these results together gives the final answer of 210. This method reinforces the understanding of place value's significance in multiplication.
Method 3: Understanding the Shift in Place Value
Multiplying any number by 10 essentially shifts each digit one place to the left in the place value system. This is because multiplying by 10 is the same as multiplying by 10¹, which represents a power of ten.
Consider 21 again:
- 2 (tens) 1 (ones)
Multiplying by 10 shifts each digit one place to the left:
- 2 (hundreds) 1 (tens)
This directly translates to 210. This method provides a powerful visual representation of how multiplication by 10 affects the place value of each digit, making it an intuitive approach for visualizing the operation.
Extending the Concept: Multiplication by Higher Powers of 10
The principles discussed above can be extended to understand multiplication by higher powers of 10 (100, 1000, etc.). Multiplying by 100 shifts each digit two places to the left, multiplying by 1000 shifts each digit three places to the left, and so on.
For example:
- 21 x 100 = 2100 (each digit shifted two places to the left)
- 21 x 1000 = 21000 (each digit shifted three places to the left)
This pattern underscores the fundamental relationship between multiplication by powers of 10 and the place value system.
Practical Applications: Real-World Examples
Understanding this type of multiplication isn't just about solving math problems; it has numerous real-world applications. Consider the following examples:
- Currency: Calculating the total cost of 21 items at $10 each involves the same principle (21 x $10 = $210).
- Measurement: Converting 21 meters to centimeters (1 meter = 100 centimeters) requires multiplying 21 by 100 (21 x 100 = 2100 centimeters).
- Data Storage: Understanding how data is organized in computer memory often involves working with powers of 10 (kilobytes, megabytes, gigabytes, etc.).
Beyond the Basics: Connecting to More Advanced Concepts
The seemingly simple problem of "2 tens 1 one x 10" serves as a foundational stepping stone to more complex mathematical concepts. It directly connects to:
- Algebra: This concept translates easily to algebraic expressions. For instance, you could represent the problem as (2x + 1) x 10, where x represents the tens place.
- Exponents and Powers: Understanding place value is inherently linked to exponents and powers of 10. The place value system itself is a representation of powers of 10.
- Scientific Notation: The efficient representation of large numbers using scientific notation relies heavily on an understanding of powers of 10 and place value.
Frequently Asked Questions (FAQ)
Q: Why is understanding place value so important?
A: Place value is the bedrock of our number system. Without understanding place value, performing even basic arithmetic operations becomes significantly more difficult. It provides the framework for understanding the value of each digit in a number, which is critical for accurate calculations.
Q: Is there a faster way to multiply by 10 besides the methods described?
A: Yes. A quick shortcut is to simply add a zero to the end of the number. This is because multiplying by 10 shifts each digit one place to the left, effectively adding a zero as a placeholder in the ones place.
Q: How does this concept apply to numbers with more than two digits?
A: The same principles apply. You can break down any number into its place values (ones, tens, hundreds, thousands, etc.) and apply the distributive property or the place value shift method to multiply by 10 or any power of 10.
Q: What if the number isn't a whole number, but includes decimals?
A: Multiplying a decimal number by 10 also shifts the decimal point one place to the right. This is because multiplying by 10 increases the value of each digit by a factor of ten.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation "2 tens 1 one x 10" provides a rich foundation for understanding fundamental mathematical concepts. By exploring different approaches to solving this problem, we've uncovered the importance of place value, the distributive property, and the relationship between multiplication and the powers of 10. This understanding isn't just about finding the correct answer (210); it's about grasping the underlying principles that govern our number system and lay the groundwork for more advanced mathematical explorations. Mastering these fundamentals empowers individuals to confidently tackle more complex mathematical challenges and apply these concepts to various real-world scenarios. The journey from a simple calculation to a profound understanding of mathematical principles showcases the beauty and power of mathematics.
Latest Posts
Latest Posts
-
How To Write An Equation For A Direct Variation
Sep 22, 2025
-
Ions Diffuse Across Membranes Through Specific Ion Channels Down
Sep 22, 2025
-
Chlorophyll Molecules Are Found In Which Part Of The Chloroplast
Sep 22, 2025
-
Least Common Multiple 5 6 7
Sep 22, 2025
-
What Is The Gcf Of 7 And 28
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 Tens 1 One X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.