2 8 18 32 18 1
faraar
Sep 17, 2025 · 6 min read
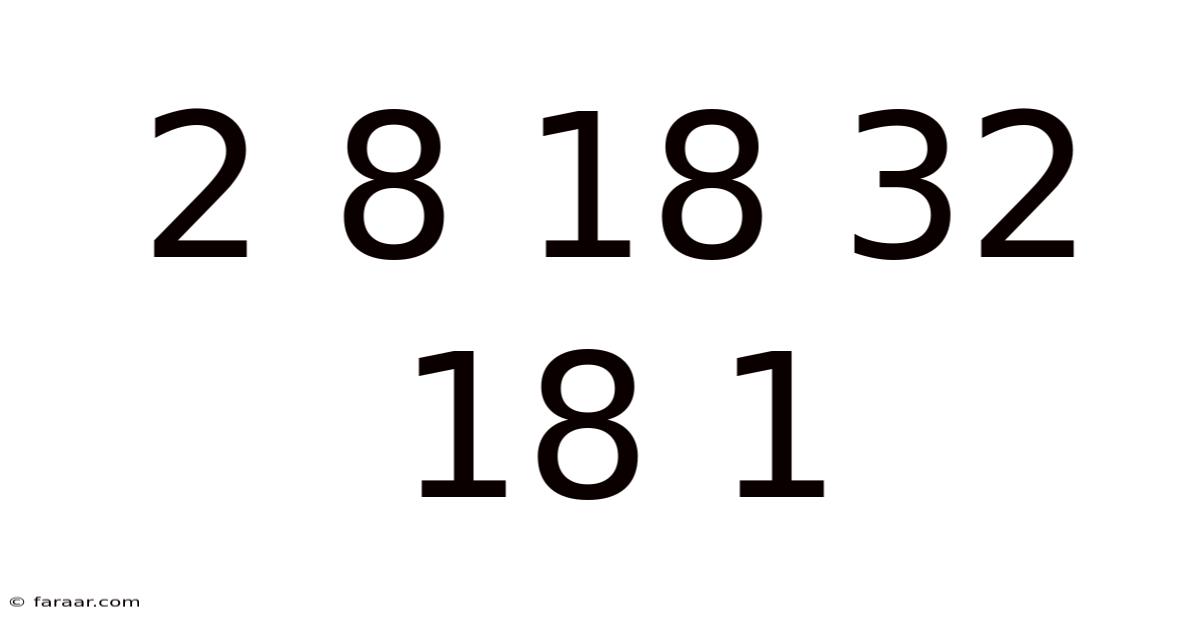
Table of Contents
Decoding the Sequence: Unveiling the Mystery Behind 2 8 18 32 18 1
This seemingly random sequence of numbers – 2, 8, 18, 32, 18, 1 – presents a fascinating puzzle. At first glance, it appears chaotic, lacking any immediately obvious pattern. However, by applying logical reasoning, mathematical principles, and a touch of creative thinking, we can uncover the underlying structure and potentially even predict future terms in the sequence. This article will delve into various approaches to analyze this number sequence, exploring different perspectives and revealing the possible mechanisms behind its generation. Understanding this seemingly simple sequence offers valuable insights into pattern recognition, problem-solving skills, and the beauty of mathematical exploration.
Understanding the Challenge: Identifying Patterns and Relationships
Before we jump into solutions, let's acknowledge the inherent ambiguity of the problem. There isn't a single, definitively "correct" answer. Multiple patterns could potentially generate this sequence. The challenge lies in finding a plausible and elegant explanation that fits the given data and allows for extrapolation. We'll explore several possible approaches, each offering a unique perspective on the sequence's structure.
Approach 1: Analyzing Differences and Second Differences
A common technique in analyzing number sequences is to examine the differences between consecutive terms. Let's start by calculating the first differences:
- 8 - 2 = 6
- 18 - 8 = 10
- 32 - 18 = 14
- 18 - 32 = -14
- 1 - 18 = -17
The first differences don't immediately reveal a clear pattern. Let's try calculating the second differences (the differences between the first differences):
- 10 - 6 = 4
- 14 - 10 = 4
- -14 - 14 = -28
- -17 - (-14) = -3
Again, the pattern remains elusive. The inconsistency in the second differences suggests that a simple linear or quadratic relationship might not be sufficient to explain the sequence. This approach highlights the need to explore more complex patterns or alternative methodologies.
Approach 2: Exploring Polynomial Relationships
While the simple difference method didn't yield conclusive results, we could explore the possibility of a higher-order polynomial relationship. This involves fitting a curve to the data points, potentially uncovering a more sophisticated pattern. This approach often requires advanced mathematical tools or software capable of polynomial regression. However, without further terms in the sequence, it's challenging to determine a definitive polynomial representation. The limited data points make it difficult to distinguish between multiple potential polynomial functions that might all fit the existing data but diverge in their predictions for future terms.
Approach 3: Investigating Recursive Relationships
Another avenue of exploration involves searching for a recursive relationship, where each term is defined in relation to the preceding terms. This type of relationship is commonly found in many mathematical sequences. However, the irregular nature of the provided sequence makes it challenging to identify a straightforward recursive formula. One might need to experiment with various combinations of previous terms and their operations to see if any consistent relationship emerges. This approach often necessitates a trial-and-error process, testing different combinations until a satisfactory recursive rule is found.
Approach 4: Considering Modular Arithmetic or Cyclical Patterns
The sequence shows a peak at 32, followed by a sharp decline. This could suggest a cyclical or modular pattern, where the numbers might repeat or follow a certain cycle after a specific number of terms. The abrupt shift from 32 to 18, and then to 1, hints at a possible break in the pattern or a transition to a different phase within a larger cycle. Further investigation into cyclical patterns, involving modulo operations or other cyclical mathematical functions, could be a promising avenue for exploring the nature of this sequence. However, the limited number of terms hinders the confirmation of such a pattern. More data points would strengthen this hypothesis or reveal its limitations.
Approach 5: Analyzing the Sequence Digit by Digit
Instead of treating the numbers as individual entities, let's consider analyzing the sequence digit by digit. We can break down each number into its constituent digits and look for patterns or relationships between these individual digits. This might reveal hidden patterns not immediately apparent when treating the numbers as whole units. This approach is particularly useful when dealing with sequences that might involve operations on individual digits rather than the numbers themselves. For example, we might look for patterns in the sum of digits, the product of digits, or other operations performed on the individual digits of each number in the sequence.
Approach 6: Considering External Factors or Contextual Information
Without additional information about the origin or context of this sequence, it's challenging to ascertain its true nature. It is possible that the sequence represents some coded information, a specific mathematical formula beyond simple arithmetic progression, or even a random collection of numbers without any underlying pattern. If there was a context associated with the sequence – for instance, if it related to a specific physical phenomenon, a mathematical problem, or a coded message – this could provide invaluable clues for deciphering the pattern.
Conclusion: The Importance of Exploration and Critical Thinking
The sequence 2, 8, 18, 32, 18, 1 presents a compelling example of how seemingly simple problems can require creative and persistent approaches to solve. While we haven't found a definitive, universally accepted answer, our exploration highlights various problem-solving techniques: from analyzing differences and exploring polynomial relationships to investigating recursive patterns and considering external factors. The absence of a single "correct" solution emphasizes the importance of critical thinking, exploration, and the acceptance of multiple potential interpretations when dealing with incomplete data or ambiguous patterns. The true beauty lies not only in finding the solution (if one exists) but also in the process of discovery and the insights gained along the way.
Further Exploration and Challenges
This analysis serves as a starting point for further investigation. Here are some avenues for continued exploration:
- Expanding the Sequence: If additional terms were provided, it would significantly aid in confirming or refuting the various hypotheses explored. More data points often bring greater clarity and constrain the possibilities.
- Advanced Mathematical Techniques: Employing more advanced mathematical techniques, such as Fourier analysis or wavelet transforms, might reveal hidden patterns or periodicities within the sequence.
- Computer Simulation and Modelling: Creating a computer simulation to test various hypotheses and systematically explore potential relationships would be a valuable tool.
- Collaboration and Peer Review: Sharing this puzzle with others and engaging in collaborative problem-solving could lead to innovative insights and alternative perspectives.
Ultimately, the challenge of deciphering the sequence 2, 8, 18, 32, 18, 1 encourages us to embrace the uncertainty inherent in problem-solving and appreciate the richness of mathematical exploration. The pursuit of understanding this seemingly simple sequence opens doors to a deeper appreciation of pattern recognition, critical thinking, and the boundless potential of mathematical analysis. The lack of a single solution highlights the multifaceted nature of problem-solving and the importance of considering multiple approaches. The journey of exploration is as valuable as the potential discovery of a definitive answer.
Latest Posts
Latest Posts
-
Can Elements Be Broken Down Into Simpler Substances
Sep 17, 2025
-
Using The Distributive Property Simplify Each Expression
Sep 17, 2025
-
Write An Equation That Represents Each Side Of The Figure
Sep 17, 2025
-
How To Check An Inverse Function
Sep 17, 2025
-
A Salsa Recipe Uses Green Pepper
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2 8 18 32 18 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.