2 3 Of A Cup Times 2
faraar
Aug 28, 2025 · 5 min read
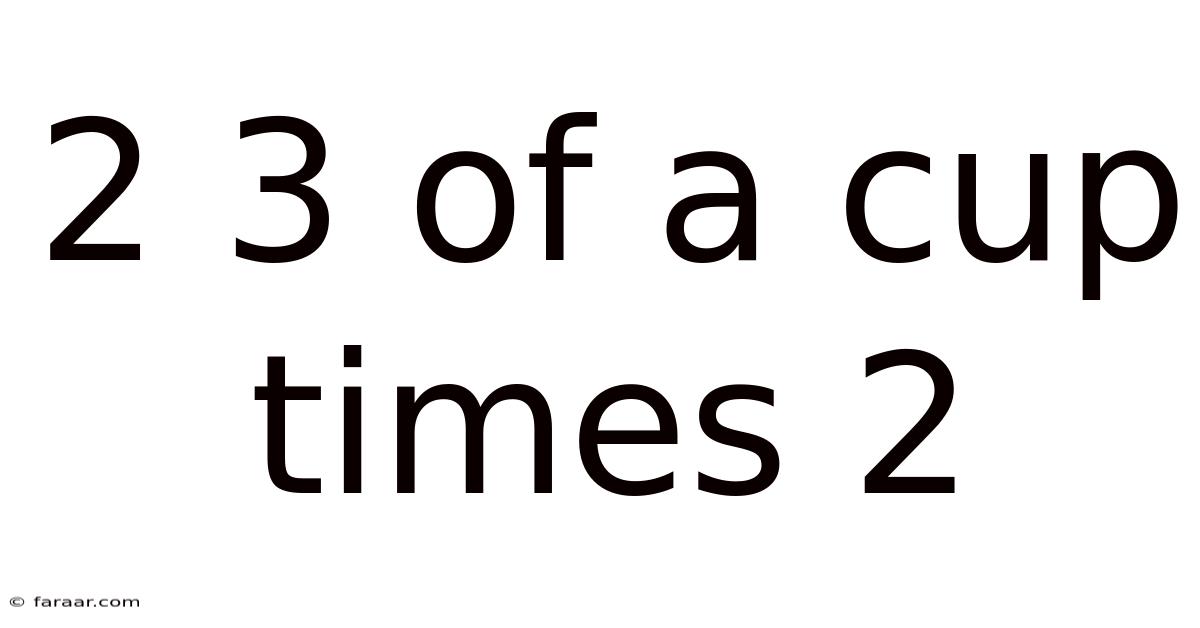
Table of Contents
Decoding the Mystery: 2/3 of a Cup Times 2
Understanding fractions and their applications in everyday life, such as in cooking or baking, is a crucial skill. This article delves into the seemingly simple calculation of "2/3 of a cup times 2," explaining the process in detail, exploring the underlying mathematical principles, and offering practical applications to solidify your understanding. We'll break down the problem step-by-step, making it accessible to anyone, regardless of their mathematical background.
Understanding the Problem: 2/3 Cup x 2
The problem "2/3 of a cup times 2" essentially asks us to double the quantity of 2/3 of a cup. This is a common scenario in cooking where a recipe calls for a certain fraction of a cup of an ingredient, and you need to double or even triple the recipe. Mastering this calculation will allow you to confidently adjust recipes and accurately measure ingredients.
Method 1: Multiplying Fractions Directly
The most straightforward method involves directly multiplying the fraction by the whole number. Remember that a whole number can be expressed as a fraction with a denominator of 1. Therefore, 2 can be written as 2/1.
Our problem becomes: (2/3) x (2/1)
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(2 x 2) / (3 x 1) = 4/3
This result, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3).
Converting Improper Fractions to Mixed Numbers
Improper fractions are often less practical in real-world applications, especially when dealing with measurements. We convert 4/3 into a mixed number, which combines a whole number and a proper fraction. To do this, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1
The whole number part of our mixed number is 1 (the quotient). The remainder (1) becomes the numerator of the proper fraction, and the denominator remains the same (3). Therefore:
4/3 = 1 1/3
So, 2/3 of a cup times 2 equals 1 1/3 cups.
Method 2: Multiplying the Numerator Only
Alternatively, you can simplify the problem by multiplying the numerator of the fraction by the whole number, keeping the denominator the same:
2/3 x 2 = (2 x 2) / 3 = 4/3
This directly gives you the improper fraction 4/3, which can then be converted to the mixed number 1 1/3 cups, as shown in the previous method. This method is often quicker for simple calculations.
Practical Applications and Real-World Examples
Let's consider some practical scenarios where this calculation is useful:
-
Doubling a Recipe: A recipe calls for 2/3 cup of flour. To double the recipe, you need 2/3 cup x 2 = 1 1/3 cups of flour.
-
Baking: A cookie recipe requires 2/3 cup of sugar. Making a double batch means you'll need 1 1/3 cups of sugar.
-
Cooking: You're making a sauce and the recipe calls for 2/3 cup of tomato paste. Doubling the recipe will require 1 1/3 cups of tomato paste.
Understanding the Mathematical Principles
The core mathematical concept at play here is the multiplication of fractions. Multiplying fractions involves multiplying the numerators and then multiplying the denominators. Converting improper fractions to mixed numbers is an essential skill for representing quantities in a more understandable and practical way, particularly when dealing with measurements. This process involves dividing the numerator by the denominator and expressing the result as a whole number and a fraction.
Frequently Asked Questions (FAQ)
-
Can I use a decimal instead of a fraction? Yes, you can convert 2/3 to its decimal equivalent (approximately 0.667) and then multiply by 2, resulting in approximately 1.334 cups. However, using fractions is often more precise, especially in cooking and baking.
-
What if I need to triple the recipe? Simply multiply 2/3 by 3: (2/3) x (3/1) = 6/3 = 2 cups.
-
How do I measure 1 1/3 cups accurately? You can use a 1-cup measuring cup and a 1/3 cup measuring cup. Alternatively, you can use a liquid measuring cup with markings for 1/3 cup and fill it accordingly.
Beyond the Basics: Working with Other Fractions
The principles discussed above apply to other fractions as well. For example, if a recipe calls for 1/4 cup of an ingredient and you need to double it, you would calculate (1/4) x 2 = 2/4 = 1/2 cup. The process remains consistent: multiply the numerators, multiply the denominators, and simplify if necessary.
Conclusion: Mastering Fractions for Everyday Use
Understanding the concept of multiplying fractions, particularly in the context of doubling quantities like 2/3 of a cup, is a valuable skill with numerous practical applications. Whether you're a seasoned baker or a novice cook, mastering these calculations will enhance your precision and confidence in the kitchen. The ability to convert between improper fractions and mixed numbers ensures accurate measurements and consistent results, transforming recipe adjustments from a daunting task into a straightforward process. By understanding the underlying mathematical principles and practicing these simple steps, you'll confidently tackle any fractional measurements that come your way. Remember, practice makes perfect! The more you work with fractions, the more comfortable and proficient you'll become. So, grab your measuring cups and start experimenting!
Latest Posts
Latest Posts
-
Write A Rule To Describe The Transformation
Aug 28, 2025
-
Rewriting Expressions Using The Distributive Property
Aug 28, 2025
-
A Car Travels On A Straight Track
Aug 28, 2025
-
Can We Use We In Research Paper
Aug 28, 2025
-
Find The Square Root Of 121
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Of A Cup Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.