2/3 Cups + 2/3 Cups Equals
faraar
Sep 17, 2025 · 5 min read
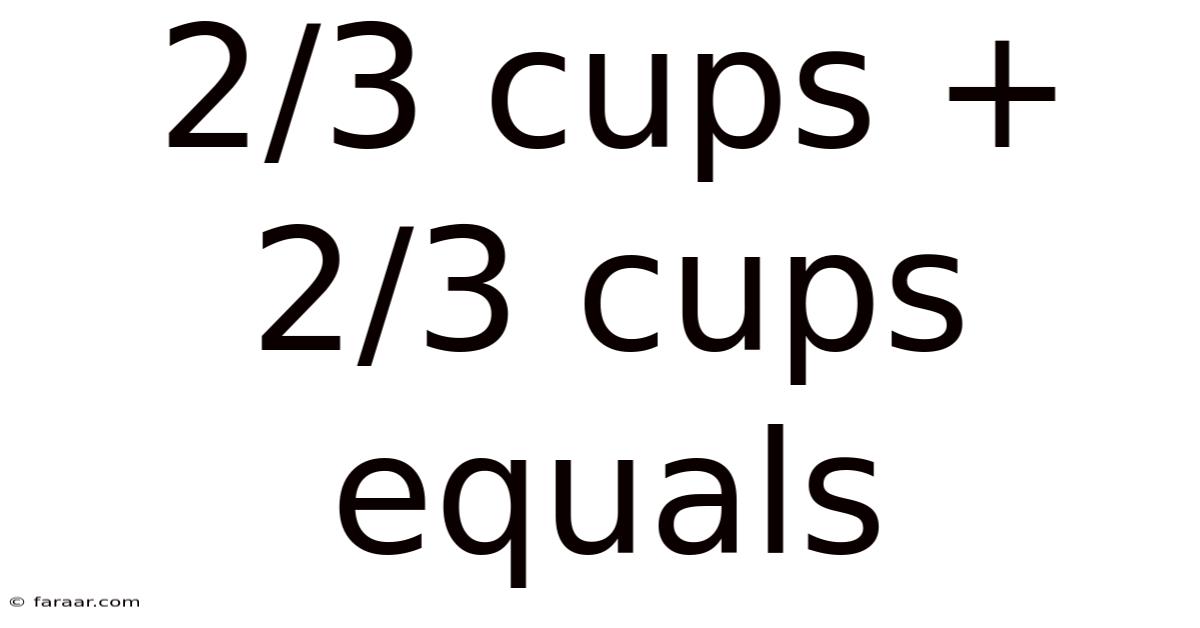
Table of Contents
2/3 Cups + 2/3 Cups Equals: A Deep Dive into Fraction Addition
This article explores the seemingly simple question: what is 2/3 cups + 2/3 cups? While the answer might seem obvious at first glance, delving deeper reveals fundamental concepts in fraction addition, crucial for various applications beyond baking and cooking. We'll cover the basic calculation, explore the underlying mathematical principles, discuss real-world applications, and address common misconceptions. By the end, you'll have a solid understanding of adding fractions, extending far beyond just measuring ingredients.
Understanding Fractions: A Quick Refresher
Before tackling the addition, let's revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts. Understanding this fundamental concept is key to adding fractions effectively.
Calculating 2/3 Cups + 2/3 Cups
Adding 2/3 cups and 2/3 cups is a straightforward process when the denominators are the same. Since both fractions share the same denominator (3), we simply add the numerators and keep the denominator unchanged.
2/3 + 2/3 = (2 + 2) / 3 = 4/3
Therefore, 2/3 cups + 2/3 cups equals 4/3 cups.
Converting Improper Fractions to Mixed Numbers
The result, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3). Improper fractions are perfectly valid mathematically, but they are often less intuitive in real-world contexts, especially when dealing with measurements. We can convert this improper fraction into a mixed number, which consists of a whole number and a proper fraction.
To convert 4/3 to a mixed number, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1
This means 4/3 is equivalent to 1 whole cup and 1/3 cup. So, the answer to our initial question can also be expressed as 1 1/3 cups.
The Importance of Common Denominators: Adding Fractions with Different Denominators
While the example above involved fractions with the same denominator, adding fractions with different denominators requires an extra step. You must find a common denominator, which is a common multiple of both denominators. Let's consider an example:
1/2 + 1/4
The denominators are 2 and 4. A common denominator is 4 (because 4 is a multiple of 2). To convert 1/2 to have a denominator of 4, we multiply both the numerator and the denominator by 2:
1/2 = (1 x 2) / (2 x 2) = 2/4
Now we can add the fractions:
2/4 + 1/4 = (2 + 1) / 4 = 3/4
This illustrates the importance of finding a common denominator before adding fractions with different denominators. The process involves equivalent fractions – fractions that represent the same value even though they look different.
Real-World Applications Beyond the Kitchen
The concept of adding fractions is far more versatile than just measuring ingredients for a recipe. It applies to numerous fields:
-
Construction and Engineering: Calculating material quantities, determining precise measurements for blueprints, and ensuring structural integrity all rely heavily on fractional calculations.
-
Finance: Calculating portions of investments, determining interest rates, and managing budgets involve understanding and manipulating fractions.
-
Data Analysis: Representing and analyzing data often involves fractions and percentages, which are fundamentally related.
-
Science: Many scientific experiments and measurements involve fractions, particularly in fields like chemistry and physics.
-
Everyday Life: Sharing items fairly, calculating distances, and understanding proportions all involve fractional concepts.
Common Misconceptions in Fraction Addition
Several common misconceptions can hinder accurate fraction addition:
-
Adding denominators directly: A common mistake is to add both the numerators and denominators directly, which is incorrect. The denominator represents the total number of parts, and it remains the same unless you're finding a common denominator.
-
Ignoring common denominators: For fractions with different denominators, failing to find a common denominator leads to an incorrect result. The fractions must be expressed with the same denominator before adding the numerators.
-
Improper fraction conversion issues: Many students struggle with converting improper fractions to mixed numbers and vice versa. Mastering this skill is crucial for accurate calculations and interpreting results in real-world contexts.
Frequently Asked Questions (FAQ)
Q: What if I have more than two fractions to add?
A: The principles remain the same. If all fractions have the same denominator, simply add the numerators and keep the denominator. If they have different denominators, find a common denominator for all fractions before adding the numerators.
Q: How do I find the least common denominator (LCD)?
A: The LCD is the smallest common multiple of all the denominators. One method is to list the multiples of each denominator until you find the smallest common multiple. Another method involves prime factorization of each denominator.
Q: Can I add fractions with different units?
A: No, you can only add fractions with the same units. For instance, you cannot directly add 2/3 cups and 1/2 liters. You would need to convert one unit to match the other before performing the addition.
Q: What if the fractions are negative?
A: The rules of adding negative numbers apply. Adding a negative fraction is the same as subtracting a positive fraction.
Conclusion: Mastering Fractions for a Brighter Future
Adding fractions, while appearing simple at first, forms a cornerstone of mathematical understanding. The example of 2/3 cups + 2/3 cups provides a practical entry point into a broader world of numerical operations. By understanding the concepts of numerators, denominators, common denominators, and the conversion between improper and mixed fractions, you equip yourself with valuable skills applicable across various disciplines and real-world situations. This knowledge is not merely about solving mathematical problems; it's about developing critical thinking and problem-solving skills crucial for success in numerous fields, from cooking and baking to engineering and finance. So, the next time you're faced with adding fractions, remember the fundamentals, and embrace the power of this seemingly simple operation.
Latest Posts
Latest Posts
-
Write Sin In Terms Of Cos
Sep 17, 2025
-
Which Has The Highest Boiling Point
Sep 17, 2025
-
Which Elements Have The Most Similar Chemical Properties
Sep 17, 2025
-
Value Of Notes In 6 8 Time Signature
Sep 17, 2025
-
What Layer Of The Earth Is Most Dense
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Cups + 2/3 Cups Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.