2 3 Cup Plus 1 2 Cup
faraar
Sep 20, 2025 · 5 min read
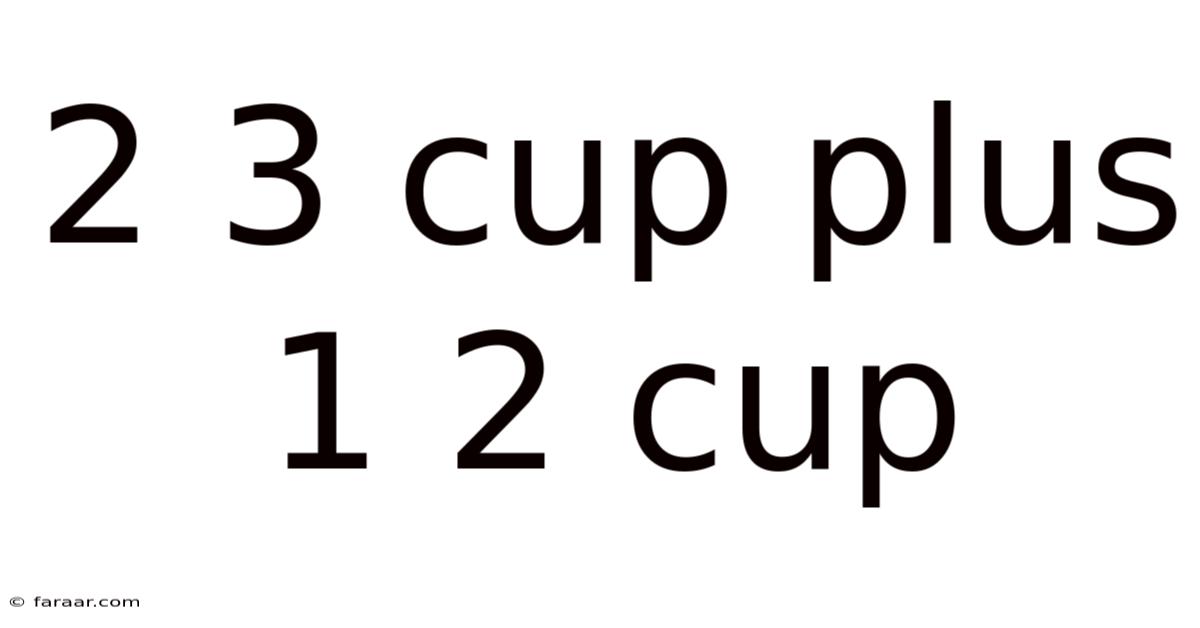
Table of Contents
Decoding the Mystery: 2 3/4 Cups Plus 1 2/3 Cups
Adding fractions, especially when they involve measurements like cups in cooking or baking, can seem daunting at first. But fear not! This comprehensive guide will break down how to solve the seemingly simple, yet surprisingly nuanced, problem of adding 2 3/4 cups plus 1 2/3 cups, explaining the process step-by-step and exploring the underlying mathematical concepts. Understanding this will help you confidently tackle similar fraction addition problems in various contexts.
Understanding Fractions: A Quick Refresher
Before we dive into the addition, let's review the basics of fractions. A fraction represents a part of a whole. It's composed of two parts:
- The numerator: The top number, indicating the number of parts you have.
- The denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator (you have 3 parts) and 4 is the denominator (the whole is divided into 4 equal parts).
Mixed numbers, like 2 3/4, combine a whole number (2 in this case) and a fraction (3/4). This means you have two whole units and three-quarters of another unit.
Step-by-Step Calculation: 2 3/4 Cups + 1 2/3 Cups
To add 2 3/4 cups and 1 2/3 cups, we need to follow these steps:
Step 1: Find a Common Denominator
The fractions 3/4 and 2/3 have different denominators (4 and 3). Before we can add them, we need to find a common denominator – a number that both 4 and 3 divide into evenly. The easiest way to find this is often to find the least common multiple (LCM). In this case, the LCM of 4 and 3 is 12.
Step 2: Convert Fractions to Equivalent Fractions
Now, we convert both fractions to equivalent fractions with the common denominator of 12:
- 3/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
- 2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
Our problem now looks like this: 2 9/12 + 1 8/12
Step 3: Add the Whole Numbers and Fractions Separately
Now, we can add the whole numbers and the fractions separately:
- Whole numbers: 2 + 1 = 3
- Fractions: 9/12 + 8/12 = 17/12
This gives us: 3 17/12
Step 4: Simplify the Result (Convert Improper Fraction to Mixed Number)
Notice that the fraction 17/12 is an improper fraction – the numerator (17) is larger than the denominator (12). We need to simplify this by converting it to a mixed number:
Divide 17 by 12: 17 ÷ 12 = 1 with a remainder of 5. This means 17/12 is equal to 1 5/12.
Step 5: Combine the Whole Numbers
Finally, add the whole number from the improper fraction to the whole number we already had: 3 + 1 = 4.
Therefore, the final answer is 4 5/12 cups.
Alternative Method: Converting Mixed Numbers to Improper Fractions First
Another approach is to convert the mixed numbers into improper fractions before adding. Let's see how this works:
Step 1: Convert Mixed Numbers to Improper Fractions
- 2 3/4: Multiply the whole number (2) by the denominator (4), add the numerator (3), and place the result over the denominator: (2 x 4) + 3 / 4 = 11/4
- 1 2/3: (1 x 3) + 2 / 3 = 5/3
Our problem now is: 11/4 + 5/3
Step 2: Find a Common Denominator and Convert Fractions
As before, the common denominator is 12:
- 11/4 becomes (11 x 3) / (4 x 3) = 33/12
- 5/3 becomes (5 x 4) / (3 x 4) = 20/12
Step 3: Add the Fractions
33/12 + 20/12 = 53/12
Step 4: Convert the Improper Fraction to a Mixed Number
53 ÷ 12 = 4 with a remainder of 5. Therefore, 53/12 = 4 5/12
The result remains the same: 4 5/12 cups.
The Importance of Accuracy in Measurement
In cooking and baking, precise measurements are crucial for achieving the desired results. A slight variation in the amount of ingredients can significantly affect the texture, taste, and overall quality of your dish. Therefore, mastering fraction addition is a valuable skill for anyone who enjoys culinary pursuits.
Practical Applications Beyond Cooking
Understanding fraction addition extends far beyond the kitchen. It's a fundamental mathematical concept applicable in various fields:
- Construction and Engineering: Calculating precise measurements for building materials, blueprints, and structural designs.
- Finance: Working with percentages, calculating interest rates, and analyzing financial data.
- Science: Measuring quantities in experiments, analyzing data, and understanding proportions.
- Sewing and Tailoring: Accurately measuring fabric and patterns for garments.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to add fractions?
A: Yes, many calculators have fraction capabilities. However, understanding the underlying process is crucial for developing a strong mathematical foundation. Using a calculator without understanding the method limits your problem-solving skills and prevents you from tackling more complex fraction problems confidently.
Q: What if I have more than two fractions to add?
A: The process remains the same. Find a common denominator for all the fractions, convert them to equivalent fractions, add the numerators, and then simplify the result if necessary.
Q: What if the fractions are negative?
A: Adding negative fractions follows the same rules as adding positive fractions, but you need to consider the rules of adding and subtracting signed numbers. Remember that adding a negative number is the same as subtracting a positive number.
Conclusion: Mastering Fraction Addition for a Brighter Future
Adding fractions, particularly mixed numbers, might seem challenging at first glance. However, by breaking down the process into manageable steps and understanding the underlying principles, you can conquer this essential mathematical skill. Whether you are a passionate baker, a budding engineer, or simply someone who wants to improve their mathematical abilities, mastering fraction addition will undoubtedly enhance your problem-solving capabilities and open doors to a broader range of opportunities. Remember the key steps: find a common denominator, convert fractions, add, and simplify. With practice, you'll find this process becomes second nature, empowering you to confidently tackle any fraction addition problem you encounter.
Latest Posts
Latest Posts
-
What Size Pizza Is 14 Inches
Sep 20, 2025
-
What Is The Exact Value Of Tan 105
Sep 20, 2025
-
Do All Rhombuses Have 2 Pairs Of Parallel Sides
Sep 20, 2025
-
How To Improve The English Pronunciation
Sep 20, 2025
-
How Much Sugar Is In A Teaspoon
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Cup Plus 1 2 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.