15 Out Of 60 As A Percentage
faraar
Aug 28, 2025 · 5 min read
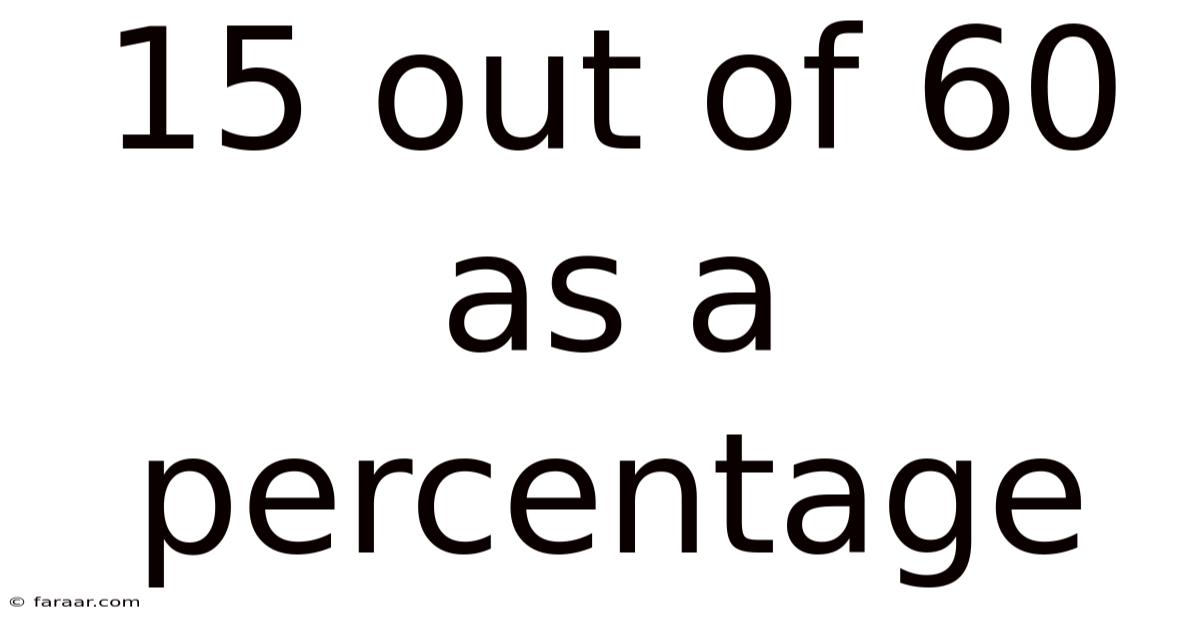
Table of Contents
15 out of 60 as a Percentage: A Comprehensive Guide to Understanding Percentages and Their Applications
Calculating percentages is a fundamental skill in various aspects of life, from academic studies to financial planning and everyday decision-making. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data, comparing values, and making informed choices. This comprehensive guide will walk you through calculating 15 out of 60 as a percentage, explain the underlying principles, and explore practical applications. We'll also cover common percentage-related problems and frequently asked questions to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." The symbol % is used to denote percentages. Therefore, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Percentages are useful for:
- Comparing proportions: Easily compare different quantities relative to a whole.
- Representing changes: Show increases or decreases in values over time.
- Understanding data: Interpret statistical information and trends effectively.
- Making calculations: Perform calculations involving discounts, taxes, interest rates, and more.
Calculating 15 out of 60 as a Percentage: Step-by-Step
To calculate 15 out of 60 as a percentage, we follow these simple steps:
Step 1: Express the ratio as a fraction:
The ratio "15 out of 60" can be expressed as the fraction 15/60.
Step 2: Simplify the fraction (optional but recommended):
Simplifying the fraction makes the calculation easier. We can divide both the numerator (15) and the denominator (60) by their greatest common divisor, which is 15:
15 ÷ 15 = 1 60 ÷ 15 = 4
This simplifies the fraction to 1/4.
Step 3: Convert the fraction to a decimal:
Divide the numerator by the denominator:
1 ÷ 4 = 0.25
Step 4: Convert the decimal to a percentage:
Multiply the decimal by 100 and add the percentage symbol (%):
0.25 x 100 = 25%
Therefore, 15 out of 60 is equal to 25%.
Different Methods for Calculating Percentages
While the above method is straightforward, there are alternative approaches you can use:
Method 1: Using Proportions:
You can set up a proportion:
15/60 = x/100
To solve for x (the percentage), cross-multiply:
60x = 1500
x = 1500/60 = 25
Therefore, x = 25%, confirming our previous result.
Method 2: Using a Calculator:
Most calculators have a percentage function. Simply enter 15 ÷ 60 and then multiply the result by 100. The calculator will directly provide the answer: 25%.
Method 3: Using the Formula:
The general formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
In this case:
(15 / 60) x 100 = 25%
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Academic performance: Calculating grades based on scores obtained in exams or assignments. For instance, if a student scores 45 out of 60 on a test, their percentage score is (45/60) x 100 = 75%.
-
Financial matters: Calculating discounts, interest rates, taxes, and profit margins. For example, a 20% discount on a $100 item means a saving of $20 (20% of $100).
-
Data analysis: Interpreting survey results, analyzing market trends, and understanding statistical data. For example, if a survey shows that 30 out of 100 respondents prefer a particular product, the percentage of respondents who prefer that product is 30%.
-
Everyday life: Calculating tips in restaurants, determining sale prices in shops, and understanding proportions in recipes.
Solving Percentage Problems: Common Scenarios
Here are some common percentage problems and how to approach them:
1. Finding the Percentage Increase or Decrease:
To calculate the percentage increase or decrease, use the following formula:
[(New Value - Old Value) / Old Value] x 100
For example, if the price of an item increases from $50 to $60, the percentage increase is [(60 - 50) / 50] x 100 = 20%.
2. Finding a Percentage of a Number:
To find a percentage of a number, convert the percentage to a decimal and multiply it by the number.
For example, to find 15% of 200, convert 15% to 0.15 and multiply it by 200: 0.15 x 200 = 30.
3. Finding the Original Value after a Percentage Change:
If you know the new value and the percentage change, you can find the original value using the following formula:
Original Value = New Value / (1 + Percentage Change/100) (for percentage increase) Original Value = New Value / (1 - Percentage Change/100) (for percentage decrease)
For example, if the price of an item is $75 after a 25% increase, the original price was $75 / (1 + 0.25) = $60.
Frequently Asked Questions (FAQ)
Q1: What if I have a more complex ratio, like 37 out of 120?
A1: Follow the same steps: (37/120) x 100 ≈ 30.83%. You can use a calculator or simplify the fraction before calculating.
Q2: How do I handle percentages greater than 100%?
A2: Percentages greater than 100% simply indicate that the part is larger than the whole. This is common when comparing growth or change over time. The calculation remains the same.
Q3: Are there any online tools or calculators to help with percentage calculations?
A3: Yes, numerous online percentage calculators are readily available. These can be useful for quick calculations or for verifying your own work. However, understanding the underlying principles is crucial for solving more complex percentage problems.
Q4: What are some common mistakes to avoid when calculating percentages?
A4: Common mistakes include incorrect order of operations, forgetting to convert percentages to decimals, and misinterpreting the meaning of percentage increase or decrease. Always double-check your calculations and make sure you understand the context of the problem.
Conclusion
Calculating percentages is a fundamental skill with broad applications across many fields. Mastering the basic principles and understanding the different methods for calculating percentages will empower you to confidently tackle various problems in your personal and professional life. This guide has provided a comprehensive overview of percentage calculations, focusing on 15 out of 60 as a percentage, along with various practical applications and troubleshooting tips. Remember to practice regularly to solidify your understanding and improve your calculation speed and accuracy. By understanding percentages, you'll be better equipped to analyze data, make informed decisions, and succeed in various aspects of life.
Latest Posts
Latest Posts
-
A Pencil And A Ruler Cost 1 50 Together
Aug 28, 2025
-
Find The Measure Of Angle G
Aug 28, 2025
-
C 5 9 F 32 Solve For F Answer
Aug 28, 2025
-
How To Do A Counter Argument
Aug 28, 2025
-
Is Endocytosis Passive Or Active Transport
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.