140 Of What Number Is 35
faraar
Sep 19, 2025 · 5 min read
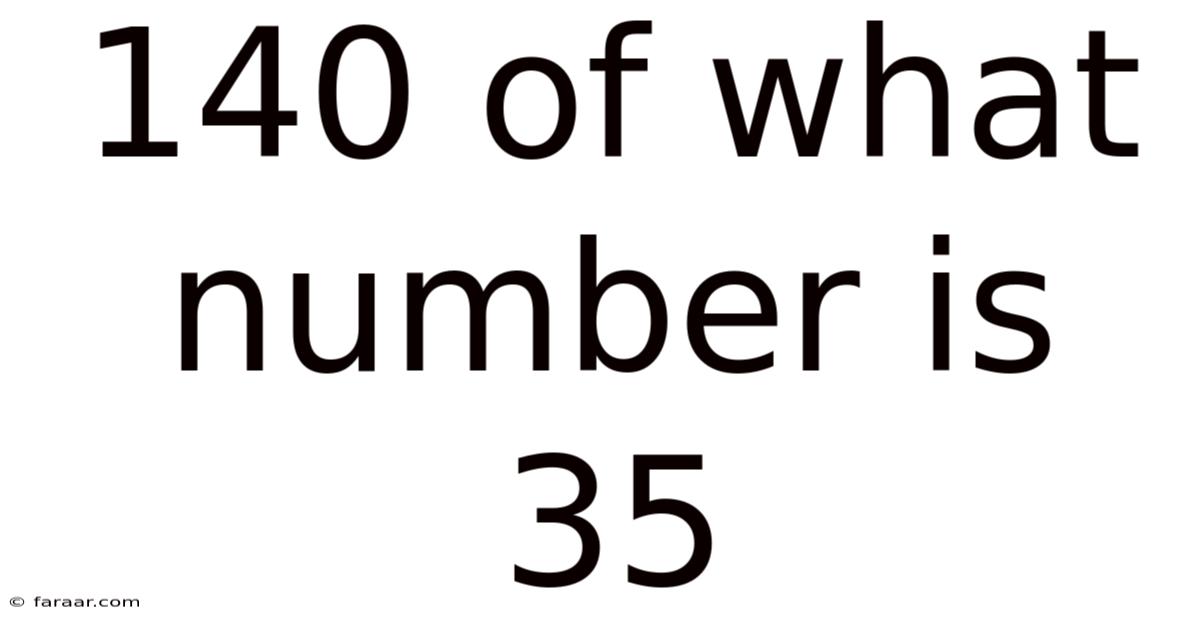
Table of Contents
140% of What Number is 35? Unraveling the Mystery of Percentages
Finding out what number 140% represents as 35 might seem like a simple math problem, but it touches upon fundamental concepts in percentages, equations, and problem-solving. This article will guide you through the process of solving this problem, explaining the underlying principles and exploring different approaches to arrive at the solution. We'll also delve into practical applications of percentage calculations and address frequently asked questions. Understanding percentage calculations is crucial in various aspects of life, from financial planning and budgeting to scientific analysis and everyday decision-making. This comprehensive guide aims to not only provide the answer but also empower you with a deeper understanding of percentages.
Understanding Percentages
Before we dive into solving "140% of what number is 35?", let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Similarly, 100% represents the whole or the entire quantity. Percentages greater than 100% indicate a quantity exceeding the original whole. In our problem, 140% means 140 out of 100, or 140/100, which simplifies to 7/5 or 1.4.
Setting up the Equation
To solve "140% of what number is 35?", we need to translate this word problem into a mathematical equation. Let's represent the unknown number as 'x'. The phrase "140% of x" can be written as 1.4x (since 140% = 1.4). The problem states that this is equal to 35. Therefore, our equation becomes:
1.4x = 35
Solving the Equation
Now we have a simple algebraic equation to solve for 'x'. To isolate 'x', we need to divide both sides of the equation by 1.4:
x = 35 / 1.4
Performing the division:
x = 25
Therefore, 140% of 25 is 35.
Alternative Methods for Solving Percentage Problems
While the above method is straightforward, there are alternative approaches to solving percentage problems. Let's explore a couple of them:
Method 1: Using Proportions
We can set up a proportion to solve this problem. A proportion is an equation that states that two ratios are equal. In this case, we can set up the proportion:
140/100 = 35/x
Cross-multiplying, we get:
140x = 3500
Dividing both sides by 140:
x = 3500 / 140 = 25
This method confirms our previous result.
Method 2: Working with Fractions
As mentioned earlier, 140% can be expressed as the fraction 7/5. Therefore, the problem can be written as:
(7/5)x = 35
To solve for x, multiply both sides by the reciprocal of 7/5, which is 5/7:
x = 35 * (5/7) = 25
Again, this method yields the same answer.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in many real-world situations. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. Understanding how percentages work is crucial for managing personal finances effectively.
-
Sales and Marketing: Businesses use percentages to track sales growth, conversion rates, market share, and customer satisfaction. Analyzing these percentages helps companies make informed decisions about pricing, promotions, and product development.
-
Science and Engineering: Percentages are used extensively in scientific research and engineering to represent experimental results, error margins, and statistical data. Accurate percentage calculations are essential for interpreting data and drawing meaningful conclusions.
-
Everyday Life: Calculating tips in restaurants, determining discounts at stores, understanding nutritional information on food labels, and interpreting statistics in news reports all involve the use of percentages.
Frequently Asked Questions (FAQs)
Q1: What if the percentage is less than 100%?
If the percentage is less than 100%, the unknown number ('x') will be larger than the given value. For example, if the problem was "20% of what number is 35?", the equation would be 0.2x = 35, and solving for x would give x = 175.
Q2: Can I use a calculator for these types of problems?
Yes, absolutely! Calculators are valuable tools for quickly performing the necessary calculations, especially when dealing with more complex percentage problems. However, understanding the underlying principles is still crucial for setting up the equation correctly.
Q3: What if the problem involves more than one unknown?
Problems involving more than one unknown require the use of simultaneous equations or other advanced algebraic techniques. These are typically covered in more advanced mathematics courses.
Q4: Are there any online resources to help me practice percentage problems?
Yes, many websites and online educational platforms offer practice problems and tutorials on percentage calculations. These resources can be very helpful in reinforcing your understanding and improving your problem-solving skills.
Q5: How can I improve my understanding of percentages?
Practice is key! The more you work with percentage problems, the more comfortable and confident you will become. Start with simple problems and gradually work your way up to more complex ones. Focus on understanding the underlying concepts and different solution methods. Don't hesitate to seek help from teachers, tutors, or online resources if you get stuck.
Conclusion
Solving "140% of what number is 35?" involves understanding the concept of percentages, translating the word problem into a mathematical equation, and using algebraic techniques to solve for the unknown. We've explored different methods to arrive at the solution (x = 25), highlighting the versatility of percentage calculations. This article has also touched upon the wide-ranging applications of percentages in various fields and addressed common questions related to percentage problems. By grasping these fundamental concepts, you'll be well-equipped to tackle a wide array of percentage-related challenges in your academic pursuits and everyday life. Remember, the key to mastering percentages is practice and a solid understanding of the underlying principles. So keep practicing, and you'll become proficient in solving percentage problems in no time!
Latest Posts
Latest Posts
-
The Sarbanes Oxley Act Of 2002 Is A Governmental Response To
Sep 19, 2025
-
Graph The Set On The Number Line
Sep 19, 2025
-
Electric Guitar Lessons Near Me For Beginners
Sep 19, 2025
-
Distributive Property And Order Of Operations
Sep 19, 2025
-
Which Statement Describes A Chemical Reaction
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 140 Of What Number Is 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.