12 Is What Percent Of 25
faraar
Sep 11, 2025 · 5 min read
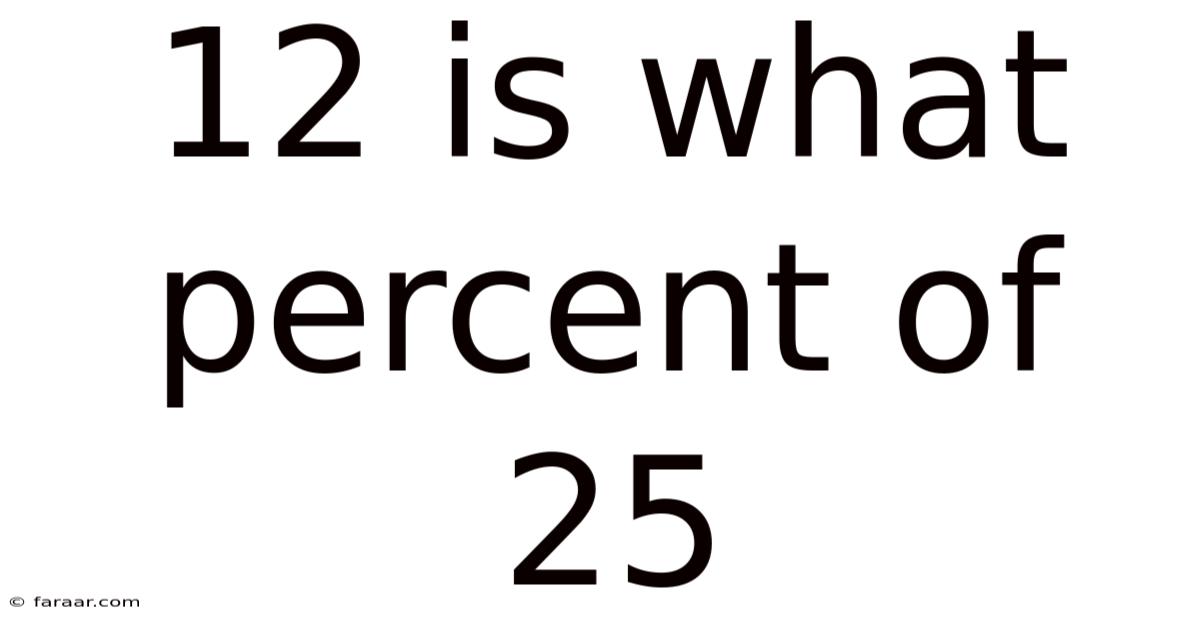
Table of Contents
12 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into how to calculate what percentage 12 represents of 25, offering a step-by-step guide, explanations, real-world applications, and addressing frequently asked questions. This will equip you not only with the answer but also with a comprehensive understanding of percentage calculations.
Introduction: Understanding Percentages
Percentages are a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Calculating percentages involves finding a proportion of a whole. In our case, we want to find what percentage 12 represents of the whole, which is 25.
Step-by-Step Calculation: Finding the Percentage
There are several ways to calculate the percentage. Here's a straightforward method:
-
Set up a proportion: We can express the problem as a proportion: 12/25 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: To solve for 'x', we cross-multiply: 12 * 100 = 25 * x
-
Simplify: This gives us 1200 = 25x
-
Solve for x: Divide both sides of the equation by 25: x = 1200 / 25
-
Calculate the result: x = 48
Therefore, 12 is 48% of 25.
Alternative Method: Using Decimal Conversion
Another approach involves converting the fraction to a decimal and then multiplying by 100:
-
Express as a fraction: Write 12 as a fraction of 25: 12/25
-
Convert to a decimal: Divide 12 by 25: 12 ÷ 25 = 0.48
-
Convert to a percentage: Multiply the decimal by 100: 0.48 * 100 = 48%
This method confirms that 12 is indeed 48% of 25.
Understanding the Mathematical Concept
The core concept behind percentage calculations is the understanding of ratios and proportions. We are essentially comparing two quantities, expressing one as a fraction of the other, and then scaling that fraction to a base of 100. This allows us to easily compare proportions regardless of the original values. The formula used in both methods above can be generalized as:
(Part / Whole) * 100% = Percentage
Where:
- Part: The number you are expressing as a percentage (in this case, 12).
- Whole: The total number (in this case, 25).
- Percentage: The result expressed as a percentage.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Here are a few examples:
-
Discounts: A store offers a 20% discount on an item priced at $50. To calculate the discount, you would find 20% of $50, which is ($50 * 0.20) = $10. The final price would be $40.
-
Taxes: Sales tax is usually expressed as a percentage. If the sales tax is 6%, and your purchase is $75, you would calculate 6% of $75, which is ($75 * 0.06) = $4.50. The total cost including tax would be $79.50.
-
Grades: School grades are often expressed as percentages. If you answered 18 out of 20 questions correctly on a test, your percentage score would be (18/20) * 100% = 90%.
-
Statistics: Percentages are extensively used to represent data in charts, graphs, and reports. For example, a company might report that 75% of its customers are satisfied with its service.
-
Finance: Interest rates on loans and investments are expressed as percentages. Compound interest calculations heavily rely on percentage calculations.
-
Science: Percentage calculations are fundamental in various scientific fields like chemistry (concentration of solutions), biology (population growth rates), and physics (efficiency of machines).
Expanding on Percentage Concepts: Finding the Whole
The problem “12 is what percent of 25?” focuses on finding the percentage. However, we can also reverse the problem. Suppose we know the percentage and the part, but we need to find the whole. Let's say 48% of a number is 12. How would we find that number?
We can set up the equation:
0.48 * x = 12
Solving for x:
x = 12 / 0.48 = 25
This shows how percentage calculations can be used to find the whole when the part and the percentage are known.
Expanding on Percentage Concepts: Finding the Part
Similarly, we can find the part if we know the whole and the percentage. Let's say we want to find 48% of 25.
We can calculate this as:
0.48 * 25 = 12
This demonstrates the flexibility of percentage calculations in solving different types of problems.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage that isn't a whole number?
A: The same principles apply. You would simply use decimals in your calculations. For example, to find what percentage 12.5 is of 25, you'd calculate (12.5/25) * 100% = 50%.
-
Q: Are there any shortcuts for calculating percentages?
A: Yes, for certain percentages like 10%, 25%, 50%, etc., you can use mental math shortcuts. For example, 10% of a number is simply that number divided by 10. 25% is that number divided by 4. These shortcuts can speed up calculations.
-
Q: What if the numbers are very large or involve decimals?
A: A calculator is your best friend in such cases. The principles remain the same, but the manual calculation might be time-consuming.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a crucial skill with widespread applications. This article provided a comprehensive guide to calculating the percentage, explained the underlying mathematical concepts, explored real-world applications, and answered frequently asked questions. By understanding the principles of ratios, proportions, and the fundamental formula, you can confidently tackle various percentage-related problems in various contexts, whether it's calculating discounts, understanding statistics, or solving problems in more complex fields. Remember to practice regularly to solidify your understanding and improve your calculation speed. With consistent practice, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
How To Start Off College Essay
Sep 11, 2025
-
Positive Negative Zero And Undefined Slope
Sep 11, 2025
-
What Is The Coefficient Of H2o
Sep 11, 2025
-
How Many Molecules Are In 25 Grams Of Nh3
Sep 11, 2025
-
How Many 9 Are In A Deck Of Cards
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.