1 Less Than Twice The Square Of A Number
faraar
Aug 29, 2025 · 5 min read
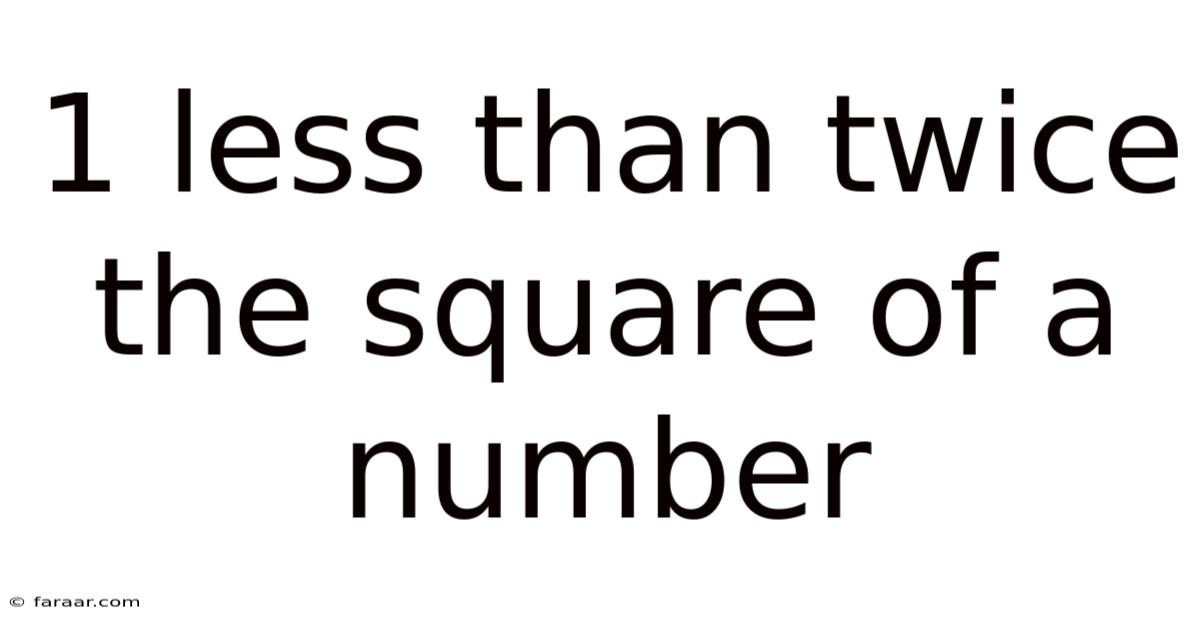
Table of Contents
Decoding "One Less Than Twice the Square of a Number": A Comprehensive Exploration
This article delves into the mathematical expression "one less than twice the square of a number," exploring its meaning, applications, and underlying mathematical concepts. We'll move beyond a simple definition, examining how this expression translates into algebraic notation, how to solve equations involving it, and its relevance in various mathematical contexts. Understanding this seemingly simple phrase unlocks a deeper appreciation for algebraic manipulation and problem-solving.
Understanding the Expression
The phrase "one less than twice the square of a number" can be broken down step-by-step to understand its meaning completely:
-
A number: This represents an unknown value, typically denoted by a variable like x or n.
-
The square of a number: This means the number multiplied by itself, represented as x² or n².
-
Twice the square of a number: This indicates multiplying the square of the number by two, resulting in 2x² or 2n².
-
One less than twice the square of a number: Finally, this means subtracting one from the result above, leading to the algebraic expression 2x² - 1 or 2n² - 1.
Translating into Algebraic Notation
The power of mathematics lies in its ability to express complex ideas concisely. The verbal description "one less than twice the square of a number" translates directly into the algebraic expression: 2x² - 1. This expression is a quadratic function, meaning the highest power of the variable x is 2. Understanding this notation is crucial for further manipulation and problem-solving.
Solving Equations Involving the Expression
Often, you'll encounter problems where this expression is part of a larger equation. Let's explore some scenarios and how to solve them.
Scenario 1: Finding the Number
Suppose the problem states: "One less than twice the square of a number is 7." This translates to the equation:
2x² - 1 = 7
To solve for x:
-
Add 1 to both sides: 2x² = 8
-
Divide both sides by 2: x² = 4
-
Take the square root of both sides: x = ±2
Therefore, the number could be either 2 or -2. This highlights the importance of considering both positive and negative solutions when dealing with square roots.
Scenario 2: More Complex Equations
Consider a more intricate equation: 2x² - 1 = x + 5
Here's how to solve it:
-
Rearrange the equation into standard quadratic form (ax² + bx + c = 0): 2x² - x - 6 = 0
-
Solve the quadratic equation: This can be done through factoring, using the quadratic formula, or completing the square. Let's use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Where a = 2, b = -1, and c = -6.
-
Substitute the values and solve:
x = [1 ± √((-1)² - 4 * 2 * -6)] / (2 * 2)
x = [1 ± √49] / 4
x = [1 ± 7] / 4
This gives two solutions: x = 2 and x = -3/2.
Graphing the Quadratic Function
The expression 2x² - 1 represents a parabola when graphed. Parabolas are U-shaped curves that are symmetrical around a vertical line called the axis of symmetry. The vertex of the parabola represents the minimum or maximum value of the function. In this case, the parabola opens upwards because the coefficient of x² (which is 2) is positive. The vertex is located at (0, -1). Understanding the graphical representation provides a visual understanding of the function's behavior and its range of values.
Applications in Real-World Scenarios
While this expression might seem abstract, it has practical applications in various fields:
-
Physics: Many physics equations involve quadratic functions, such as those describing projectile motion or the relationship between distance, time, and acceleration.
-
Engineering: Engineers use quadratic equations to model curves and shapes in design and construction.
-
Economics: Quadratic functions can be used to model cost functions, revenue functions, and profit maximization problems.
-
Computer Science: Quadratic equations are fundamental in algorithms and data structures, particularly in optimization problems.
Further Exploration: Variations and Extensions
The core concept of "one less than twice the square of a number" can be extended and modified in various ways:
-
Adding constants: We could add or subtract other constants to the expression, creating variations like 2x² - 1 + 5 or 2x² - 1 - 10.
-
Multiplying by constants: Multiplying the entire expression by a constant changes the shape and scale of the parabola. For example, 3(2x² - 1) would stretch the parabola vertically.
-
Adding linear terms: Including a linear term (like +3x) would shift the parabola and alter its vertex. This would result in a more complex quadratic expression.
Frequently Asked Questions (FAQ)
Q: What if the number is negative?
A: The expression works equally well for both positive and negative numbers. Squaring a negative number results in a positive number, so the overall effect is still a quadratic function.
Q: Can this expression be used with other operations?
A: Yes, the expression can be incorporated into more complex equations involving addition, subtraction, multiplication, and division. The methods for solving such equations would depend on the specific equation.
Q: What are the limitations of this expression?
A: The expression itself has no inherent limitations, but the context in which it's used might impose restrictions. For instance, if the expression represents a physical quantity, it might only be valid within a certain range of values.
Q: How can I improve my understanding of quadratic equations?
A: Practice solving a variety of quadratic equations, explore graphical representations, and understand the different methods of solving them (factoring, quadratic formula, completing the square).
Conclusion
The seemingly simple phrase "one less than twice the square of a number" opens a door to a rich world of mathematical concepts. From understanding algebraic notation and solving quadratic equations to appreciating the graphical representation and real-world applications, this exploration reveals the depth and power of mathematical expressions. By mastering this fundamental concept, you lay a strong foundation for tackling more advanced mathematical challenges. Remember, the key to success lies in breaking down complex problems into smaller, manageable steps, and consistently practicing your skills. This understanding of quadratic functions and their applications provides a strong stepping stone for further mathematical exploration and problem-solving across a variety of fields.
Latest Posts
Latest Posts
-
How Many Ounces Are In 5 Lbs
Sep 01, 2025
-
St Labre Indian School Charity Rating
Sep 01, 2025
-
Common Factors Of 7 And 14
Sep 01, 2025
-
Using The Circle Below Find Each Arc Length
Sep 01, 2025
-
How Far Can You Walk In 2 Hours
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about 1 Less Than Twice The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.