1 And 3 4 Times 3
faraar
Sep 08, 2025 · 5 min read
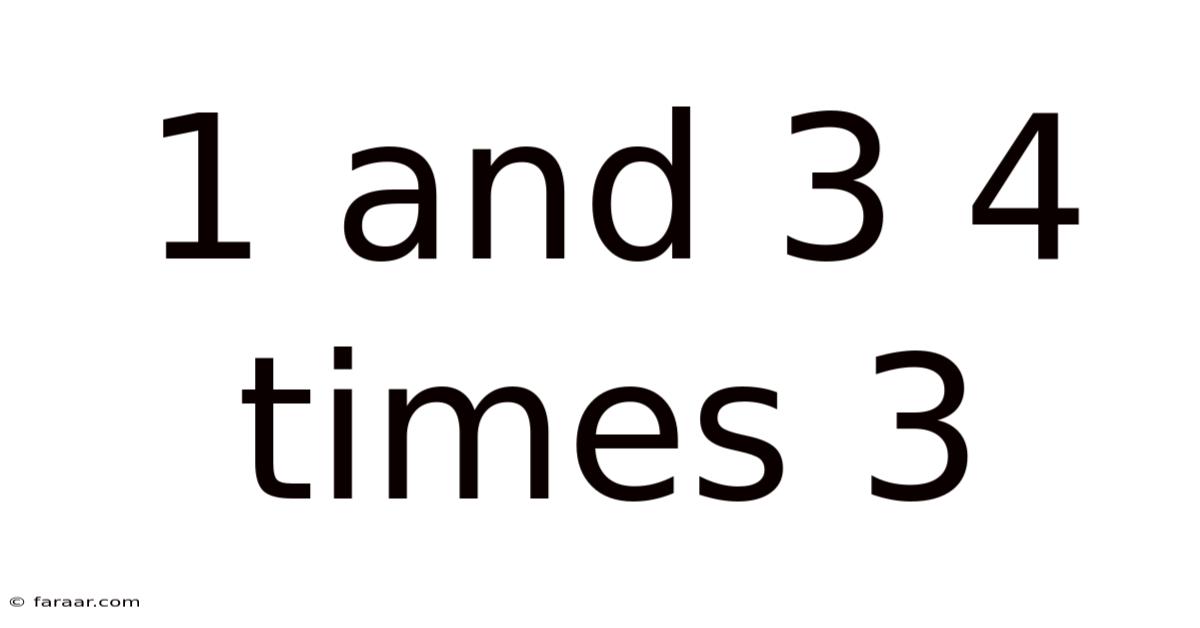
Table of Contents
Decoding the Mathematical Puzzle: 1 and 3, 4 Times 3
This article delves into the seemingly simple yet surprisingly multifaceted mathematical expression: "1 and 3, 4 times 3". At first glance, it might appear straightforward, a basic arithmetic problem. However, unpacking this phrase reveals a deeper exploration of mathematical interpretation, order of operations, and even the nuances of language itself. We’ll examine various interpretations, break down the process step-by-step, explore the underlying principles, and address frequently asked questions. This comprehensive guide aims to not only solve the problem but also enhance your understanding of fundamental mathematical concepts.
Understanding the Ambiguity: The Power of Language
The phrase "1 and 3, 4 times 3" is deliberately ambiguous. The lack of explicit mathematical symbols forces us to consider different interpretations. This ambiguity highlights the importance of precise mathematical notation. In mathematics, clarity is paramount to avoid misunderstandings. The way we express mathematical ideas significantly impacts the result.
Let's explore the potential interpretations:
Interpretation 1: (1 + 3) x (4 x 3)
This interpretation treats "1 and 3" as 1 + 3, and "4 times 3" as a separate multiplication. This follows a natural grouping based on the commas. Following the order of operations (PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), we get:
- Parentheses/Brackets: (1 + 3) = 4 and (4 x 3) = 12
- Multiplication: 4 x 12 = 48
Therefore, under this interpretation, the answer is 48.
Interpretation 2: 1 + (3 x 4 x 3)
This interpretation takes "4 times 3" to mean that 3 is multiplied by 4 and then added to 1. Here, the comma is less of a separator and more of a slight pause in the spoken expression. The order of operations dictates:
- Multiplication: (3 x 4 x 3) = 36
- Addition: 1 + 36 = 37
In this case, the solution is 37.
Interpretation 3: (1 + 3) x 3 x 4
This interpretation treats the entire phrase as a chain of multiplications and additions. The commas are practically ignored here, with the 'and' acting as a simple plus sign.
- Addition: (1 + 3) = 4
- Multiplication: 4 x 3 x 4 = 48
This approach also yields 48 as the result. Note that while the result is the same as Interpretation 1, the underlying process differs slightly.
The Importance of Order of Operations (PEMDAS/BODMAS)
The discrepancies in our interpretations highlight the crucial role of the order of operations. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are mnemonics to remember the sequence of operations. Without a clear understanding and application of these rules, we can arrive at different and incorrect answers. In mathematical notation, this ambiguity is eliminated through the use of parentheses and other symbols.
For example, writing the expression as (1 + 3) × (4 × 3) removes any ambiguity and clearly indicates the intended calculation. Similarly, 1 + (3 × 4 × 3) removes any confusion. The use of clear and unambiguous mathematical notation is essential for correct calculations and communication.
Exploring Further Mathematical Concepts
While the initial problem focuses on basic arithmetic, we can use this as a springboard to explore more advanced concepts:
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. Although not directly applicable to our interpretations above, understanding this property is vital in more complex algebraic manipulations.
-
Associative Property: This property states that (a + b) + c = a + (b + c) and (a × b) × c = a × (b × c). This is implicitly used in our calculations, demonstrating that the order in which we perform addition or multiplication within a set of parentheses does not alter the final result.
-
Commutative Property: This property states that a + b = b + a and a × b = b × a. This means the order of numbers in addition or multiplication doesn't change the result. This is evident in our interpretations where the order of multiplication in (4 x 3) doesn't affect the outcome.
Addressing Frequently Asked Questions (FAQs)
Q: Why are there different answers?
A: The different answers stem from the ambiguity inherent in the phrasing of the problem. The lack of explicit mathematical notation allows for multiple valid interpretations, each leading to a different result. This emphasizes the importance of precise mathematical language.
Q: What is the "correct" answer?
A: There isn't a single "correct" answer without further clarification on the intended meaning of the phrase. Each interpretation we explored is mathematically sound based on its own assumptions.
Q: How can I avoid this ambiguity in the future?
A: Always use precise mathematical notation. Parentheses, brackets, and other symbols remove any doubt about the intended order of operations. For example, (1 + 3) x (4 x 3) is unambiguous.
Q: Is this a trick question?
A: It's not necessarily a trick question, but it highlights the importance of clarity in mathematical communication. It serves as a good exercise to understand the nuances of mathematical interpretation and the necessity of precise language.
Conclusion: The Value of Precise Communication
The exploration of "1 and 3, 4 times 3" transcends simple arithmetic. It serves as a valuable lesson in the importance of precise communication and the critical role of mathematical notation. The ambiguity inherent in the phrasing highlights the need for clear and unambiguous expression when dealing with mathematical concepts. This seemingly simple problem has unveiled deeper understandings of order of operations, fundamental mathematical properties, and the importance of clear communication in mathematics. Through this detailed analysis, we've not only solved the problem in its various interpretations but also enhanced our comprehension of core mathematical principles, emphasizing the significance of precise language and notation in avoiding confusion and ensuring accuracy in calculations. This example serves as a powerful reminder for anyone engaging in mathematics, regardless of skill level – clarity and precision are paramount.
Latest Posts
Latest Posts
-
Verify That F And G Are Inverse Functions Algebraically
Sep 08, 2025
-
Does A Triangle Have Perpendicular Sides
Sep 08, 2025
-
Left Handed Guitar Lessons Near Me
Sep 08, 2025
-
Is The Experimental Group The Independent Variable
Sep 08, 2025
-
2x 3y 6 Slope Intercept Form
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 1 And 3 4 Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.