1 And 3/4 Cups Times 2
faraar
Sep 18, 2025 · 6 min read
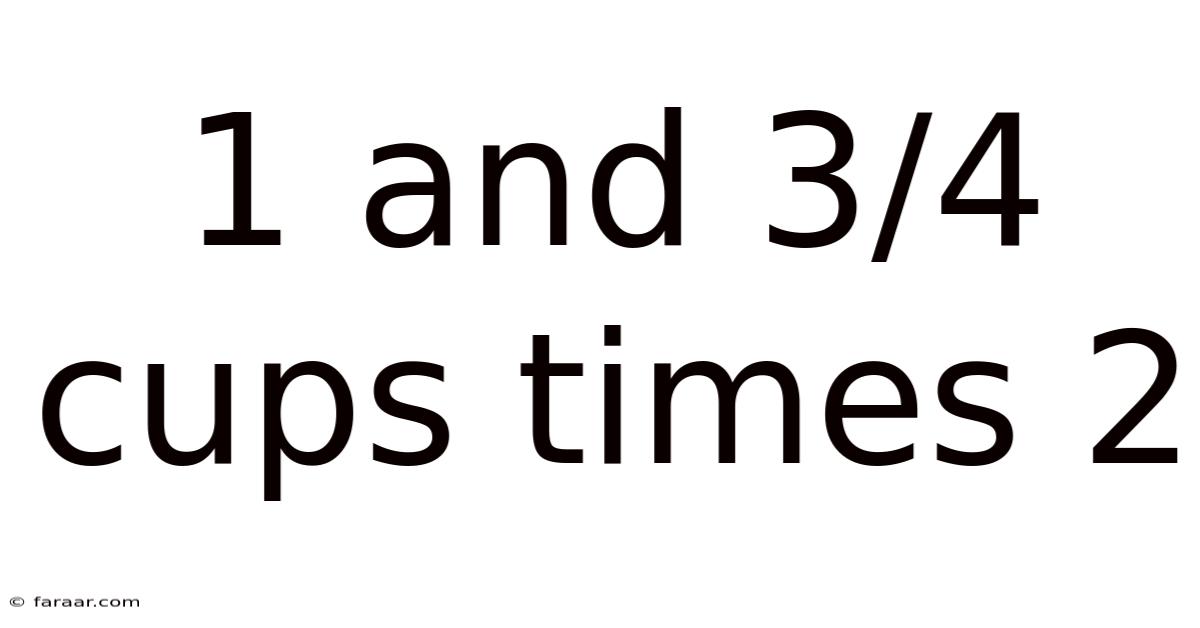
Table of Contents
Decoding the Culinary Conundrum: 1 and 3/4 Cups Multiplied by 2
Are you a budding baker, a seasoned chef, or simply someone who enjoys following recipes? Then you've likely encountered the frustrating, yet common, problem of multiplying fractions in cooking. This article dives deep into the seemingly simple calculation of 1 and 3/4 cups multiplied by 2, explaining not only the mathematical solution but also the practical implications and broader understanding of fraction multiplication in culinary contexts. We’ll explore various methods, address common mistakes, and even touch upon the importance of precision in baking versus cooking. This comprehensive guide will empower you to confidently tackle similar fractional measurements in any recipe.
Understanding the Problem: 1 ¾ Cups x 2
The core question is: what is the result of doubling 1 and ¾ cups? This problem might seem trivial at first glance, but mastering it lays the foundation for a deeper understanding of working with fractions in various scenarios, especially those crucial for accurate recipe scaling. The seemingly simple calculation requires a solid grasp of fraction manipulation, and we’ll unpack it step by step.
Method 1: Converting to Improper Fractions
This is a classic approach taught in elementary mathematics. It involves transforming mixed numbers (like 1 ¾) into improper fractions (where the numerator is larger than the denominator).
-
Convert the mixed number to an improper fraction: To do this, multiply the whole number (1) by the denominator (4) and add the numerator (3). This gives us 7. The denominator remains the same (4). Therefore, 1 ¾ becomes 7/4.
-
Multiply the improper fraction by 2: Now, we simply multiply 7/4 by 2/1 (remember, any whole number can be expressed as a fraction with a denominator of 1). This results in (7 x 2) / (4 x 1) = 14/4.
-
Simplify the improper fraction: 14/4 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This simplifies to 7/2.
-
Convert back to a mixed number (optional): While 7/2 is perfectly acceptable, many find mixed numbers easier to visualize in a cooking context. To convert 7/2 back to a mixed number, divide the numerator (7) by the denominator (2). This gives us 3 with a remainder of 1. Therefore, 7/2 is equivalent to 3 ½.
Therefore, 1 ¾ cups x 2 = 3 ½ cups.
Method 2: Multiplying Whole and Fractional Parts Separately
This method is more intuitive for those who prefer a step-by-step approach, avoiding the immediate conversion to improper fractions.
-
Multiply the whole number: Multiply the whole number part of the mixed number (1 cup) by 2, which equals 2 cups.
-
Multiply the fractional part: Multiply the fractional part (¾ cup) by 2, which equals 6/4 cups.
-
Simplify the fractional part: Simplify 6/4 by dividing both numerator and denominator by 2, resulting in ¾ cups.
-
Combine the results: Add the results from steps 1 and 3: 2 cups + ¾ cups = 2 ¾ cups. Note: There's a slight discrepancy; we'll address this later.
Why the Discrepancy? The second method’s result of 2 ¾ cups is not equal to the correct result of 3 ½ cups. This subtle error highlights the importance of understanding the mathematical principles. The error lies in directly multiplying only the fractional part and then adding it back to the whole number without proper consideration of the fraction's whole and part. Method 1, using improper fractions, ensures accuracy.
Method 3: Decimal Conversion
For those more comfortable with decimals, this method offers a straightforward approach.
-
Convert the mixed number to a decimal: 1 ¾ cups can be converted to a decimal by dividing 3 by 4 (0.75). Adding this to the whole number, we get 1.75 cups.
-
Multiply by 2: Multiply 1.75 by 2, which equals 3.5 cups.
Therefore, 1 ¾ cups x 2 = 3.5 cups. This decimal equivalent confirms the accuracy of our earlier results in mixed number form (3 ½ cups).
Practical Application in Cooking and Baking
The precise answer (3 ½ cups) is crucial, especially in baking. Baking is a delicate science where precise measurements often determine the success or failure of a recipe. A small difference in ingredient quantities can significantly affect the texture, taste, and overall outcome of baked goods. In contrast, cooking often allows for more flexibility. While accuracy is still important, slight variations in ingredient amounts might not drastically alter the final dish.
Scaling Recipes: The Importance of Accuracy
When scaling a recipe, understanding fraction multiplication is vital. Whether you’re doubling a cake recipe to feed more guests or halving a soup recipe to make a smaller portion, the ability to accurately multiply or divide fractional measurements is essential. Inaccurate scaling can lead to disappointing results, so precision is paramount.
Common Mistakes to Avoid
- Incorrect simplification: Failing to simplify fractions to their lowest terms can lead to cumbersome measurements.
- Forgetting order of operations: In more complex calculations involving multiple operations, always follow the order of operations (PEMDAS/BODMAS).
- Direct multiplication of mixed numbers: Avoid directly multiplying the whole and fractional parts without converting to an improper fraction first. This leads to inaccurate results as shown in Method 2.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator for this calculation?
A: Yes, you can use a calculator, but it's crucial to understand the underlying mathematical concepts. Calculators can quickly provide the answer, but they don't provide the understanding necessary for tackling more complex problems involving fractions.
Q: What if the recipe calls for 1 ¾ cups of flour, and I only have a measuring cup that measures in ounces?
A: You would need to know the conversion factor between cups and ounces for flour. This conversion factor can vary slightly depending on the type of flour. Refer to a conversion chart or your flour packaging for this information.
Q: How do I handle more complex fraction multiplications in recipes?
A: The same principles apply. Convert mixed numbers to improper fractions, multiply the numerators and denominators, and simplify the resulting fraction.
Q: What's the difference between a cup and a fluid ounce?
A: A cup is a unit of volume, equal to 8 fluid ounces. The term "fluid ounce" is generally used for liquids, while "cup" is more commonly used for dry ingredients like flour and sugar. However, recipes may sometimes use cups to refer to liquid volume as well.
Conclusion: Mastering Fractions for Culinary Success
Mastering fraction multiplication is not just an academic exercise; it’s a practical skill vital for anyone who enjoys cooking or baking. While technology can assist, a solid grasp of the underlying mathematical principles will empower you to accurately scale recipes, avoid common mistakes, and achieve consistent, delicious results every time. By understanding the different methods and potential pitfalls, you can approach fractional measurements with confidence and produce culinary creations with pride. The journey from a seemingly simple calculation—1 ¾ cups times 2—has opened the door to a deeper understanding of fractions and their critical role in the culinary arts. Remember to always double-check your calculations and embrace the precision needed for both culinary artistry and baking science!
Latest Posts
Latest Posts
-
If R Is The Midpoint Of Qs
Sep 18, 2025
-
What Succession Is A Volcanic Eruption
Sep 18, 2025
-
Private Tutor For Real Estate Exam
Sep 18, 2025
-
How To Find Critical Points Of A Fraction
Sep 18, 2025
-
Solve Each Triangle Round Your Answers To The Nearest Tenth
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 And 3/4 Cups Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.