1/8 Divided By 1/2 As A Fraction
faraar
Sep 11, 2025 · 6 min read
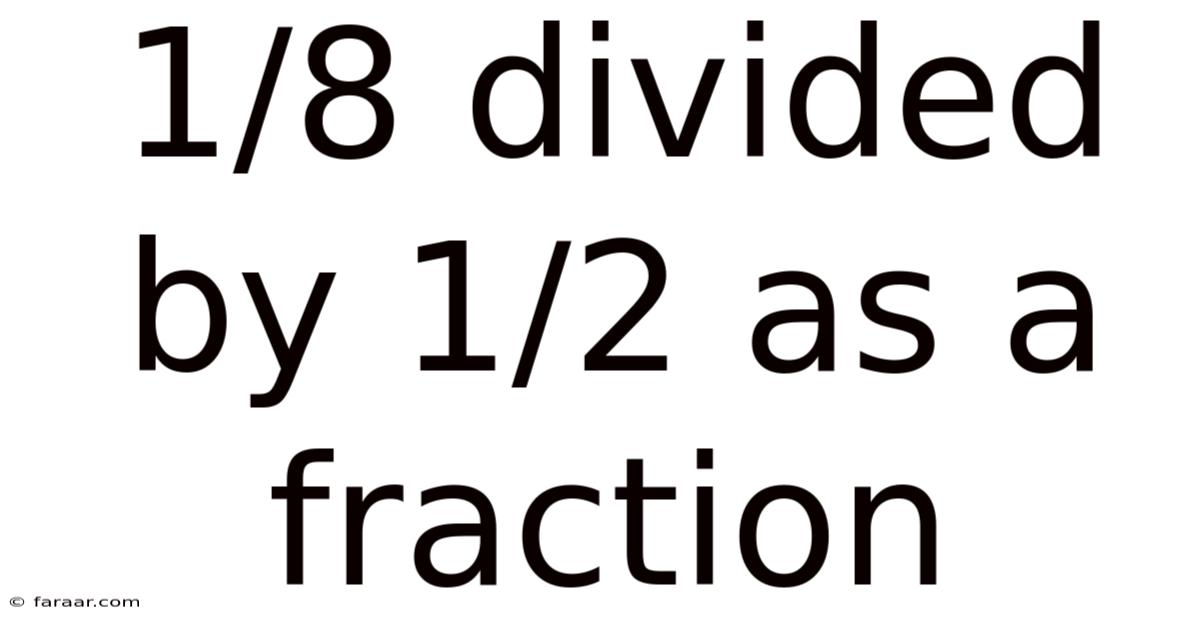
Table of Contents
Understanding 1/8 Divided by 1/2: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This article will delve into the seemingly simple problem of 1/8 divided by 1/2, explaining not just the solution but the underlying mathematical principles. We'll explore multiple approaches, address common misconceptions, and provide a solid foundation for tackling more complex fraction division problems. By the end, you'll not only know the answer to 1/8 ÷ 1/2 but also possess the confidence to tackle any fraction division challenge.
Introduction: Why Fraction Division Matters
Fractions represent parts of a whole, and understanding how to manipulate them is crucial in various fields, from baking and cooking to engineering and finance. Dividing fractions, in particular, allows us to solve problems involving splitting quantities into smaller parts or determining how many times one fraction fits into another. This skill is a cornerstone of mathematical literacy and opens doors to more advanced mathematical concepts. This article focuses on the specific problem of 1/8 divided by 1/2, but the principles discussed are applicable to a wide range of fraction division problems. Mastering this will empower you to confidently approach more intricate calculations.
Method 1: The "Keep, Change, Flip" Method (or Invert and Multiply)
This is arguably the most popular and easiest method for dividing fractions. It's based on the principle that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down.
Here's how it works for 1/8 divided by 1/2:
- Keep: Keep the first fraction as it is: 1/8
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (find its reciprocal): 1/2 becomes 2/1.
So, the problem becomes: 1/8 × 2/1
- Multiply: Multiply the numerators (top numbers) together: 1 × 2 = 2
- Multiply: Multiply the denominators (bottom numbers) together: 8 × 1 = 8
Therefore, the answer is 2/8.
- Simplify: This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2. 2 ÷ 2 = 1 and 8 ÷ 2 = 4.
Final Answer: 1/4
This method provides a quick and efficient way to solve fraction division problems. Its simplicity makes it accessible to learners of all levels.
Method 2: Using a Common Denominator
While the "Keep, Change, Flip" method is efficient, understanding the underlying principle of division can be enhanced by using a common denominator. This method relies on the fact that dividing two fractions with a common denominator simplifies to dividing the numerators.
-
Find a Common Denominator: The least common multiple (LCM) of 8 and 2 is 8.
-
Rewrite the Fractions: Rewrite both fractions with the common denominator of 8:
- 1/8 remains as 1/8
- 1/2 becomes 4/8 (multiply both numerator and denominator by 4)
-
Divide the Numerators: Now, divide the numerators: 1 ÷ 4 = 1/4
Final Answer: 1/4
Method 3: Visual Representation with Models
Visual aids can greatly enhance understanding, especially for beginners. Let's visualize 1/8 divided by 1/2 using a model.
Imagine a circle divided into 8 equal slices. 1/8 represents one of these slices. Now, consider the question: "How many 1/2 portions are there in 1/8?" A half of the circle would consist of 4 slices.
Visually, you can see that one 1/8 slice is a quarter (1/4) of a 1/2 portion (4 slices). Therefore, 1/8 divided by 1/2 equals 1/4.
Explanation with Scientific Reasoning and Mathematical Principles
The methods above demonstrate different approaches to solving 1/8 ÷ 1/2. However, understanding the core mathematical principle reinforces the validity of the result. Division is essentially the inverse operation of multiplication. When we divide a number a by a number b, we're looking for a number c such that b × c = a.
In our case, a = 1/8 and b = 1/2. We are searching for c such that (1/2) × c = 1/8.
By multiplying both sides of the equation by 2 (the reciprocal of 1/2), we get:
2 × (1/2) × c = 2 × (1/8)
This simplifies to:
c = 2/8 = 1/4
This algebraic manipulation confirms that the answer, obtained using the "Keep, Change, Flip" method or the common denominator method, is indeed 1/4.
Addressing Common Misconceptions
One common mistake is to simply divide the numerators and the denominators separately. This would result in (1 ÷ 1) / (8 ÷ 2) = 1/4, which coincidentally yields the correct answer in this specific case. However, this approach is incorrect for most fraction division problems and shouldn't be relied upon. It's essential to use the correct methods outlined above for accurate results.
Frequently Asked Questions (FAQ)
-
Q: Can I divide fractions using a calculator? A: Yes, most calculators have a fraction function that allows for direct fraction division. However, understanding the manual methods is crucial for developing a strong grasp of the underlying mathematical principles.
-
Q: What if the fractions are mixed numbers? A: Convert mixed numbers into improper fractions before applying the division methods. For example, 1 1/2 would become 3/2.
-
Q: What happens if the result is an improper fraction? A: Leave the answer as an improper fraction or convert it into a mixed number, depending on the context of the problem.
-
Q: Why does the "Keep, Change, Flip" method work? A: This method is a shortcut based on the reciprocal property of multiplication and division. Dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Q: Is there only one correct method to solve this problem? A: No, there are several mathematically sound methods, and the best approach depends on individual preferences and the complexity of the problem.
Conclusion: Mastering Fraction Division
Dividing fractions might seem challenging initially, but with a systematic approach and a solid understanding of the underlying principles, it becomes a manageable skill. The problem of 1/8 divided by 1/2, while seemingly simple, provides an excellent platform to explore different methods and deepen your understanding of fraction manipulation. Remember the "Keep, Change, Flip" method for its efficiency, but also appreciate the value of understanding the common denominator approach and the visual representation for a more holistic grasp of the concept. By mastering these techniques, you'll build a strong foundation for tackling more complex mathematical problems in the future. The ability to confidently divide fractions will serve you well in various aspects of life, solidifying your mathematical skills and boosting your problem-solving capabilities. Don't hesitate to practice with various examples to reinforce your understanding and build your confidence.
Latest Posts
Latest Posts
-
How Many Cm Is A Mile
Sep 11, 2025
-
What Is The Solution To Mc014 1 Jpgmc014 2 Jpgmc014 3 Jpgmc014 4 Jpgmc014 5 Jpg
Sep 11, 2025
-
Factors Of That Add Up To 1
Sep 11, 2025
-
How To Use Commas With Quotes
Sep 11, 2025
-
Ions In Polar Solvents Quick Check
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1/8 Divided By 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.