1/6 + 1/2 As A Fraction
faraar
Sep 17, 2025 · 6 min read
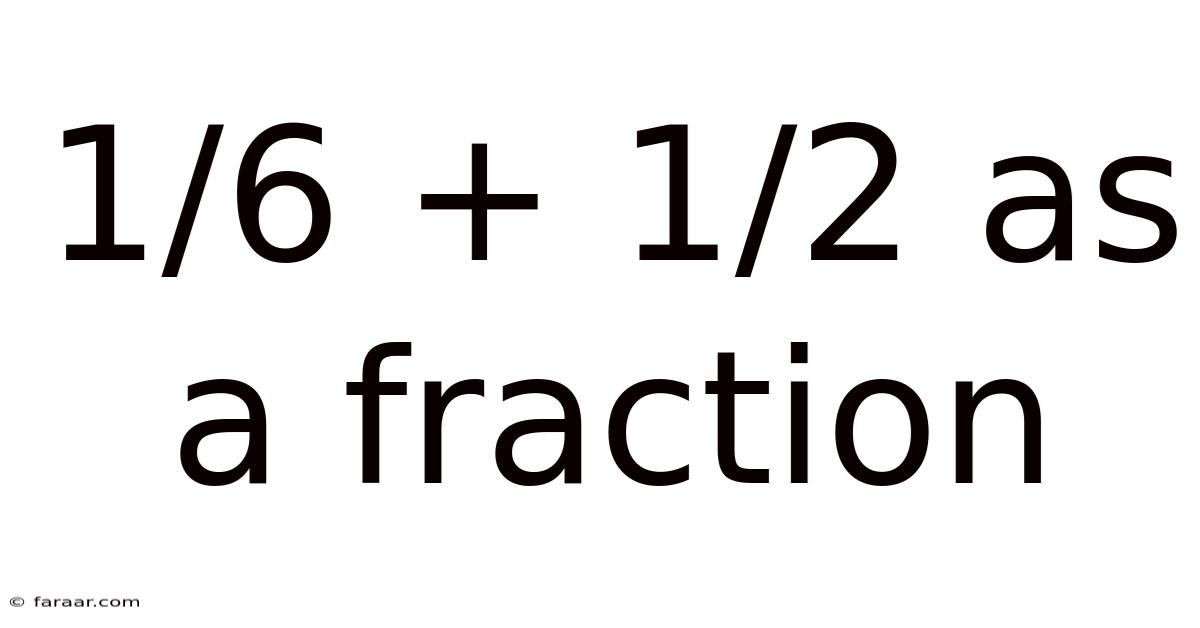
Table of Contents
Mastering Fractions: A Deep Dive into 1/6 + 1/2
Adding fractions might seem like a simple task, but understanding the underlying principles is crucial for mastering more complex mathematical concepts. This comprehensive guide will walk you through the process of adding 1/6 and 1/2, explaining not only the steps involved but also the underlying mathematical reasoning. We'll explore different methods, address common misconceptions, and delve into the broader world of fraction arithmetic. By the end, you'll not only know the answer to 1/6 + 1/2 but also possess a solid foundation for tackling any fraction addition problem.
Understanding Fractions: A Quick Recap
Before diving into the addition, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/6, the denominator 6 signifies that the whole is divided into six equal parts, and the numerator 1 indicates that we are considering only one of those parts. Similarly, 1/2 represents one out of two equal parts.
Adding Fractions: The Fundamental Principle
The core principle behind adding fractions lies in finding a common denominator. This is because you can only add or subtract fractions that represent parts of the same whole. Imagine trying to add one-sixth of a pizza to one-half of a different, larger pizza – it wouldn't make sense! To add them, we need to express both fractions as parts of the same-sized whole.
The common denominator is a multiple of both denominators. The easiest common denominator to find is usually the least common multiple (LCM) of the denominators. Finding the LCM is crucial for simplifying the resulting fraction.
Method 1: Finding the Least Common Multiple (LCM)
To add 1/6 + 1/2, we first need to find the LCM of 6 and 2.
- Multiples of 6: 6, 12, 18, 24, 30…
- Multiples of 2: 2, 4, 6, 8, 10, 12…
The smallest number that appears in both lists is 6. Therefore, the LCM of 6 and 2 is 6. This will be our common denominator.
Method 2: Converting to Equivalent Fractions
Now that we have our common denominator (6), we need to convert both fractions so they have this denominator.
-
Converting 1/2: To change the denominator of 1/2 to 6, we multiply both the numerator and the denominator by 3 (because 2 x 3 = 6). This gives us (1 x 3) / (2 x 3) = 3/6. Note that multiplying both the numerator and denominator by the same number doesn't change the value of the fraction; it only changes its representation.
-
Converting 1/6: 1/6 already has a denominator of 6, so we don't need to change it.
Now our addition problem becomes: 1/6 + 3/6
Performing the Addition
With both fractions having the same denominator, we can now add them. To add fractions with the same denominator, we simply add the numerators and keep the denominator the same:
1/6 + 3/6 = (1 + 3) / 6 = 4/6
Simplifying the Fraction
The final step is to simplify the resulting fraction. This means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD of 4 and 6 is 2.
Dividing both the numerator and denominator by 2, we get:
4/6 = (4 ÷ 2) / (6 ÷ 2) = 2/3
Therefore, 1/6 + 1/2 = 2/3
Visual Representation
It's helpful to visualize this process. Imagine a rectangle divided into six equal parts. 1/6 represents one of these parts. Now, imagine another rectangle of the same size, divided into two equal parts. 1/2 represents one of those two parts. If we divide the second rectangle into six equal parts as well, we see that 1/2 is equivalent to 3/6. Combining one-sixth from the first rectangle with three-sixths from the second gives us a total of four-sixths, which simplifies to two-thirds.
Alternative Method: Using Improper Fractions
Another approach involves converting the fractions to improper fractions first. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
-
Converting 1/6: This is already a proper fraction (numerator less than denominator).
-
Converting 1/2: This is also a proper fraction.
While we don't need to convert these to improper fractions for this specific problem, this method becomes more useful when dealing with mixed numbers (a whole number and a fraction). Let's illustrate with a similar, slightly more complex example: 1 1/6 + 1/2
First convert the mixed number to an improper fraction: 1 1/6 = (1 x 6 + 1)/6 = 7/6
Then find the common denominator (6) and rewrite the fractions: 7/6 + 3/6 = 10/6
Finally simplify the resulting fraction: 10/6 = 5/3 = 1 2/3
Addressing Common Mistakes
A common mistake is adding both the numerators and the denominators directly: 1/6 + 1/2 ≠ 2/8. This is incorrect because you are not adding like terms. Remember, you can only add the numerators after finding a common denominator. Always focus on getting that common denominator first.
Frequently Asked Questions (FAQs)
-
Q: Can I use any common denominator, or does it have to be the least common multiple (LCM)?
A: You can use any common denominator, but using the LCM simplifies the process, resulting in a fraction that requires less simplification at the end.
-
Q: What if the fractions have different signs (one positive, one negative)?
A: The process remains the same, except you follow the rules of adding integers. For example, 1/6 + (-1/2) would involve finding a common denominator (6), converting -1/2 to -3/6, and then adding: 1/6 + (-3/6) = -2/6 = -1/3.
-
Q: How can I practice more fraction addition problems?
A: You can find numerous online resources, workbooks, and educational apps that offer practice problems on fraction addition and other fraction operations. Start with simple problems and gradually increase the difficulty.
Conclusion
Adding fractions, particularly seemingly simple ones like 1/6 + 1/2, requires a solid understanding of the fundamental principles. By consistently following the steps – finding a common denominator, converting to equivalent fractions, adding the numerators, and simplifying – you can confidently tackle any fraction addition problem. Remember the visualization – it helps to truly grasp the concept. With practice and a clear understanding of the underlying math, mastering fractions becomes easier, opening doors to more advanced mathematical concepts. So, keep practicing, and remember: 1/6 + 1/2 = 2/3.
Latest Posts
Latest Posts
-
What Is The Molecular Mass Of Co
Sep 17, 2025
-
What Is The Length Of Line Segment Gh
Sep 17, 2025
-
20 Miles Is How Many Hours
Sep 17, 2025
-
A Comparison Between Two Unlike Things Using Like Or As
Sep 17, 2025
-
Write The Ordered Pairs For The Relation
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/6 + 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.