1/4 Divided By 2 In Fraction
faraar
Sep 21, 2025 · 6 min read
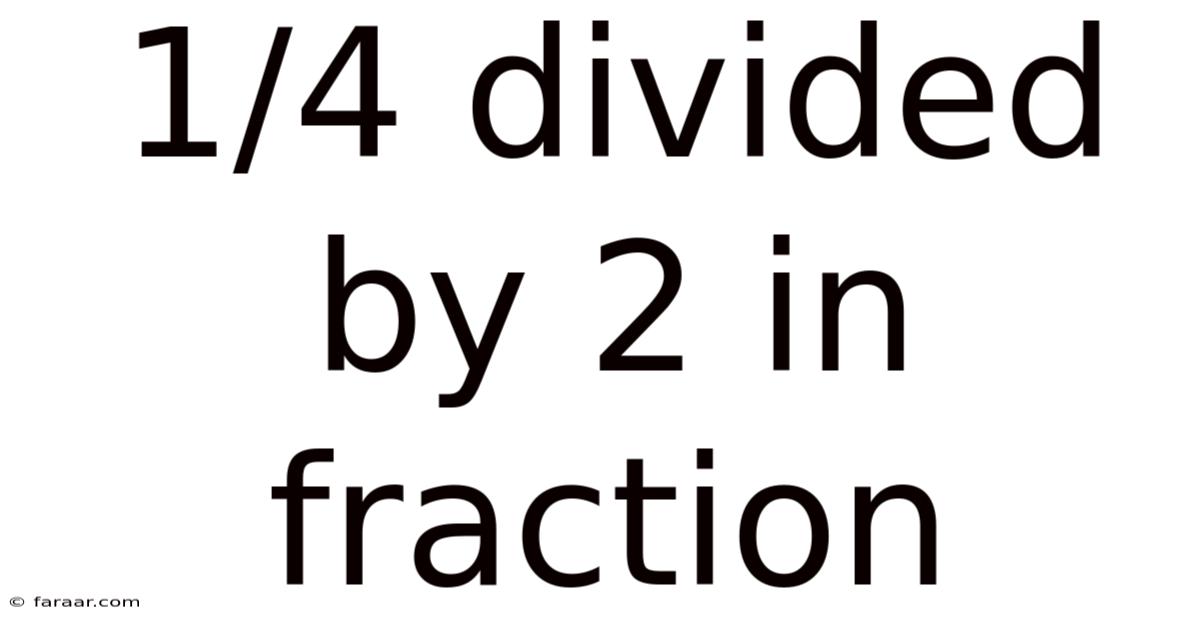
Table of Contents
Understanding 1/4 Divided by 2: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This article will guide you through dividing the fraction 1/4 by 2, explaining the steps involved, the underlying mathematical principles, and offering practical examples to solidify your understanding. This comprehensive guide will cover various methods and address frequently asked questions, ensuring you master this fundamental concept in mathematics. We'll delve into both the procedural and conceptual aspects, making this a valuable resource for students and anyone looking to refresh their knowledge of fractions.
Introduction to Fraction Division
Before tackling 1/4 divided by 2, let's establish a solid foundation in fraction division. Unlike addition and subtraction, where we need common denominators, dividing fractions involves a different approach. The core principle lies in reciprocating (inverting) the second fraction and then multiplying. This is because division is essentially the inverse operation of multiplication. Remember, reciprocating a fraction means switching the numerator and the denominator. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5 is 1/5 (since 5 can be expressed as 5/1).
Step-by-Step Solution: 1/4 Divided by 2
Now, let's solve 1/4 divided by 2 step-by-step. We can express 2 as a fraction: 2/1. Therefore, our problem becomes:
1/4 ÷ 2/1
Step 1: Reciprocate the second fraction.
The reciprocal of 2/1 is 1/2.
Step 2: Change the division sign to a multiplication sign.
Our equation now transforms into:
1/4 × 1/2
Step 3: Multiply the numerators and the denominators.
Multiply the numerators together (1 × 1 = 1) and the denominators together (4 × 2 = 8).
This gives us:
1/8
Therefore, 1/4 divided by 2 equals 1/8.
Visualizing the Division: A Practical Approach
Understanding fractions visually can significantly enhance comprehension. Imagine you have a pizza sliced into four equal pieces (quarters). You have one of those slices (1/4). Now, you want to divide that single slice among two people. Each person would receive one-eighth of the original pizza (1/8). This visual representation perfectly illustrates the result of 1/4 divided by 2.
The Mathematical Rationale: Why Does Reciprocating Work?
The method of reciprocating and multiplying stems from the fundamental relationship between multiplication and division. Consider the equation:
a ÷ b = x
This means that 'x' is the number which, when multiplied by 'b', gives 'a'.
Now, let's express 'b' as a fraction (b/1). To solve for 'x', we can use the following logic:
a ÷ (b/1) = x
Multiplying both sides by the reciprocal of (b/1), which is (1/b), we get:
a × (1/b) = x × (b/1) × (1/b)
The (b/1) and (1/b) cancel each other out, simplifying the equation to:
a × (1/b) = x
This demonstrates why reciprocating the second fraction and multiplying provides the correct solution for fraction division.
Solving Similar Problems: Applying the Method
Now that you've grasped the method, let's try some similar problems:
-
3/5 ÷ 3: First, express 3 as 3/1. The reciprocal is 1/3. So, 3/5 × 1/3 = 1/5.
-
1/2 ÷ 1/4: The reciprocal of 1/4 is 4/1 (or simply 4). So, 1/2 × 4 = 4/2 = 2.
-
2/3 ÷ 5/6: The reciprocal of 5/6 is 6/5. So, 2/3 × 6/5 = 12/15. This can be simplified to 4/5 by dividing both numerator and denominator by 3 (their greatest common divisor).
These examples demonstrate the consistent application of the reciprocate-and-multiply method. Remember to always simplify your final answer to its lowest terms whenever possible.
Dealing with Mixed Numbers: A Step-by-Step Guide
Sometimes, you might encounter mixed numbers in division problems. A mixed number is a combination of a whole number and a fraction (e.g., 1 1/2). To divide fractions involving mixed numbers, you need to convert the mixed numbers into improper fractions before applying the reciprocate-and-multiply method.
Let's consider an example:
2 1/2 ÷ 1/4
Step 1: Convert mixed numbers to improper fractions.
2 1/2 is equivalent to (2 × 2 + 1)/2 = 5/2.
Step 2: Reciprocate the second fraction.
The reciprocal of 1/4 is 4/1 (or 4).
Step 3: Multiply the fractions.
5/2 × 4/1 = 20/2 = 10
Therefore, 2 1/2 ÷ 1/4 = 10.
Understanding the Concept of Division as Repeated Subtraction
While reciprocating and multiplying is the most efficient method for fraction division, it's helpful to understand the underlying concept of division as repeated subtraction. Let's reconsider 1/4 ÷ 2. This can be interpreted as: "How many times can you subtract 1/2 from 1/4?" The answer is obviously not a whole number because 1/2 is larger than 1/4. The process of reciprocation and multiplication provides the fractional equivalent of this repeated subtraction.
Frequently Asked Questions (FAQ)
Q1: Why do we reciprocate the second fraction and multiply?
A1: This is a consequence of the relationship between multiplication and division. Reciprocating and multiplying effectively reverses the division operation, leading to the correct solution. The mathematical proof presented earlier demonstrates this relationship.
Q2: What if the divisor is a whole number?
A2: Treat the whole number as a fraction with a denominator of 1 (e.g., 3 becomes 3/1). Then, follow the standard reciprocate-and-multiply method.
Q3: How do I simplify my answer?
A3: Find the greatest common divisor (GCD) of the numerator and the denominator. Divide both the numerator and the denominator by the GCD to obtain the simplified fraction.
Q4: Can I use a calculator to solve fraction division problems?
A4: Many calculators can handle fraction calculations directly. However, understanding the manual method is crucial for a deeper understanding of the underlying mathematical principles.
Conclusion: Mastering Fraction Division
Dividing fractions, including problems like 1/4 divided by 2, might seem challenging initially. However, by understanding the step-by-step process of reciprocating the divisor and multiplying, you can master this fundamental mathematical concept. This article has provided not only the procedural steps but also the underlying mathematical reasoning and practical applications, equipping you with the knowledge and confidence to tackle various fraction division problems. Remember to practice consistently to reinforce your understanding and build fluency in solving these types of problems. The more you practice, the easier it will become, and the more comfortable you will be with manipulating fractions in various mathematical contexts.
Latest Posts
Latest Posts
-
Is The Acoustic Guitar Hard To Learn
Sep 21, 2025
-
Difference Between A Homonym And A Homophone
Sep 21, 2025
-
33 And 1 3 As A Decimal
Sep 21, 2025
-
How Many Sides Does A Convex Polygon Have
Sep 21, 2025
-
How Do You Find Excluded Values
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.