1 3 1 2 In Fraction Form
faraar
Sep 16, 2025 · 6 min read
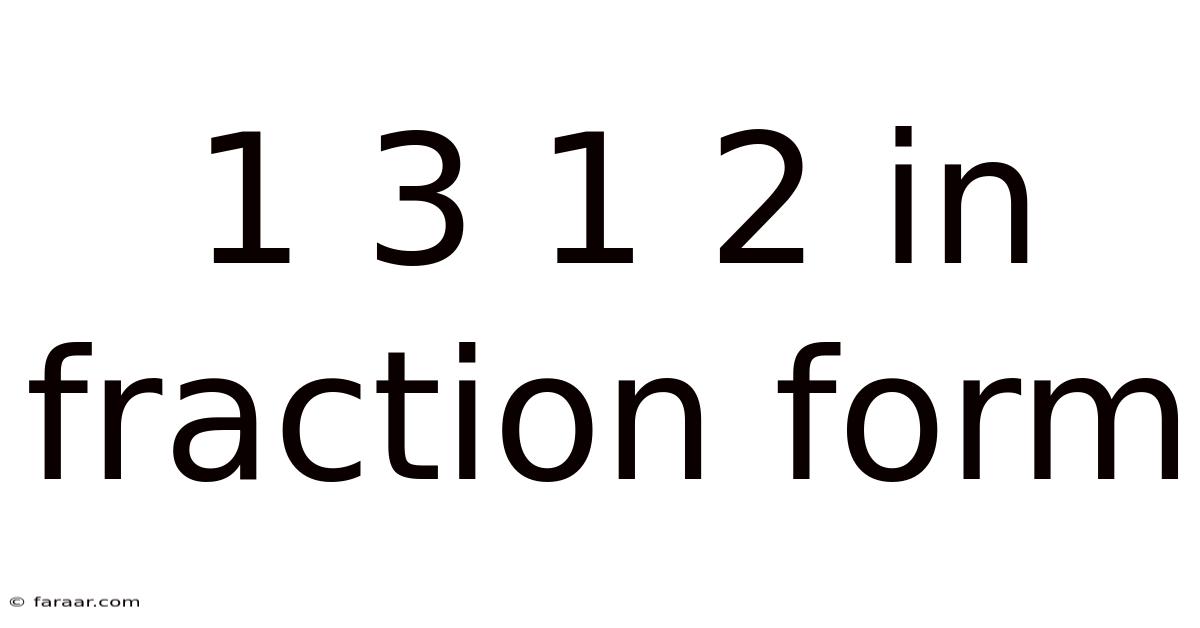
Table of Contents
Decoding the Mystery of 1 3 1 2 in Fraction Form: A Comprehensive Guide
The seemingly simple sequence "1 3 1 2" might appear innocuous at first glance. However, interpreting this sequence as a mixed number and converting it into an improper fraction presents a fascinating exploration of mathematical principles. This article will delve into the intricacies of converting mixed numbers to improper fractions, focusing specifically on the example 1 3 1 2, while also providing a broader understanding of fraction manipulation. We'll unravel the steps, explore the underlying mathematical concepts, and answer frequently asked questions, ensuring a comprehensive understanding for readers of all mathematical backgrounds.
Understanding Mixed Numbers and Improper Fractions
Before we tackle our specific sequence, let's establish a clear understanding of the fundamental concepts. A mixed number combines a whole number and a proper fraction. For example, 2 ¾ is a mixed number, representing two whole units and three-quarters of another unit. An improper fraction, on the other hand, has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). For instance, 11/4 is an improper fraction because the numerator (11) is larger than the denominator (4). Both mixed numbers and improper fractions represent the same quantitative value; they are simply different ways of expressing it.
Interpreting "1 3 1 2" as a Mixed Number
The sequence "1 3 1 2" requires careful interpretation. It's crucial to understand that this isn't a single mixed number presented in a non-standard format. Instead, it's likely representing two separate numbers: 1 3/1 and 2. This interpretation becomes clear when considering typical mathematical notation conventions. We'll address the possibility of misinterpretations later in the FAQ section.
Therefore, we will proceed by first addressing the conversion of the mixed number 1 3/1 into an improper fraction. Then, we'll discuss how this relates to the '2' in the original sequence, exploring various interpretations.
Converting 1 3/1 to an Improper Fraction: A Step-by-Step Guide
The conversion from a mixed number to an improper fraction involves a straightforward process:
-
Multiply the whole number by the denominator: In our example, the whole number is 1, and the denominator is 1. 1 x 1 = 1.
-
Add the result to the numerator: The numerator of our fraction is 3. Adding the result from step 1, we get 1 + 3 = 4.
-
Keep the same denominator: The denominator remains 1.
-
Write the result as an improper fraction: Combining the results, we get the improper fraction 4/1.
Therefore, the mixed number 1 3/1 is equivalent to the improper fraction 4/1. Note that 4/1 is simply another way of representing the whole number 4.
Interpreting the "2" in the Sequence "1 3 1 2"
Now that we've converted 1 3/1 to 4/1 (or 4), let's consider how this interacts with the "2" in the original sequence. There are several possible interpretations:
-
Addition: The sequence might represent the addition of two numbers: 4 + 2 = 6. In this case, the final answer, expressed as an improper fraction, would be 6/1.
-
Separate Numbers: The sequence could represent two distinct values, 4 and 2, not necessarily requiring any mathematical operation between them.
-
A More Complex Expression: A more complex mathematical operation may be implied, potentially involving multiplication, division, or other mathematical processes, but without more context, we cannot determine a unique interpretation.
Mathematical Explanation: The Logic Behind the Conversion
The conversion process from a mixed number to an improper fraction is rooted in the fundamental understanding of fractions as representing parts of a whole. A mixed number directly shows the whole units and the remaining fractional part. Converting to an improper fraction simply combines all these parts into a single fraction. Multiplying the whole number by the denominator accounts for the total number of parts represented by the whole units, effectively converting them into the same fractional units as the remaining fraction. Adding the numerator then incorporates the remaining fractional part, creating a single representation of the whole quantity.
Frequently Asked Questions (FAQ)
Q1: Could "1 3 1 2" represent a different mixed number?
A1: It's highly unlikely. Standard mathematical notation uses a space or a whole-number symbol to separate the whole number part from the fractional part of a mixed number. Interpreting "1 3 1 2" as a single mixed number would require a non-standard notation. The most probable interpretation involves two separate numbers as previously described.
Q2: What if the sequence meant 1 31/2?
A2: If the sequence is intended to represent the mixed number 1 31/2, the conversion to an improper fraction would involve a slightly different process.
- Multiply the whole number by the denominator: 1 x 2 = 2.
- Add the result to the numerator: 2 + 31 = 33.
- Keep the same denominator: The denominator remains 2.
- Write the result as an improper fraction: This gives us the improper fraction 33/2.
Q3: How can I convert an improper fraction back to a mixed number?
A3: To convert an improper fraction back to a mixed number, you perform the reverse operation:
-
Divide the numerator by the denominator: For example, with 33/2, 33 ÷ 2 = 16 with a remainder of 1.
-
The quotient becomes the whole number: 16 is the whole number.
-
The remainder becomes the numerator of the fraction: 1 is the new numerator.
-
The denominator remains the same: The denominator remains 2.
-
Write the result as a mixed number: This results in the mixed number 16 ½.
Q4: Are there any real-world applications for converting mixed numbers to improper fractions?
A4: Yes, converting between mixed numbers and improper fractions is crucial in various real-world applications, especially in cooking, construction, and engineering. For example, when measuring ingredients in a recipe or calculating the amount of material needed for a project, converting between these forms ensures accurate calculations and avoids errors. It’s also fundamental in higher-level mathematical concepts such as algebra and calculus.
Conclusion
Converting the sequence "1 3 1 2" into a fraction form requires a careful interpretation of the given sequence, as it likely represents two separate numbers rather than a single mixed number. This exercise highlights the importance of understanding mathematical notation and the relationship between mixed numbers and improper fractions. The conversion process itself, however, is a fundamental skill with wide-ranging applications in mathematics and everyday life. Mastering this conversion is a critical step towards a more comprehensive understanding of fractions and their significance in mathematical operations. Remember to always pay close attention to the context and notation used to ensure accurate interpretation and calculation.
Latest Posts
Latest Posts
-
Is 1 4 Half Of 1 2 Cup
Sep 16, 2025
-
Diagram Of All The Frequencies Of The Elements
Sep 16, 2025
-
Is Lino3 Acidic Basic Or Neutral
Sep 16, 2025
-
Two Reactions And Their Equilibrium Constants Are Given
Sep 16, 2025
-
What Does It Mean When You See In A Cell
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 3 1 2 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.