1 2 4 8 16 32 64
faraar
Sep 23, 2025 · 6 min read
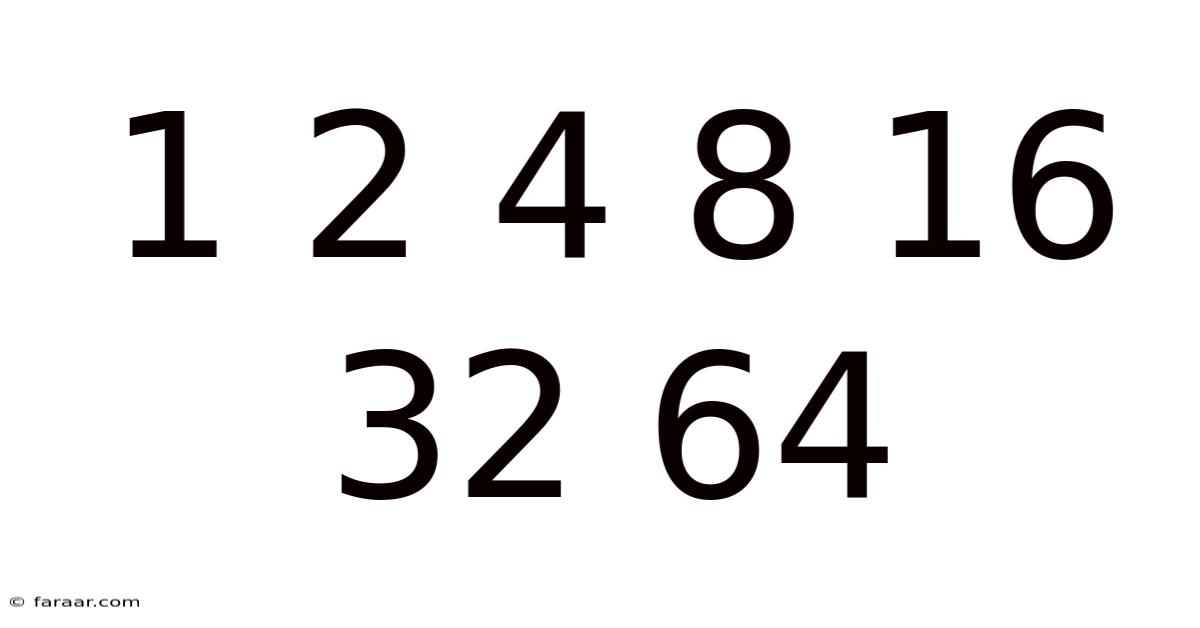
Table of Contents
Decoding the Power of Two: Exploring the Sequence 1, 2, 4, 8, 16, 32, 64... and Beyond
The seemingly simple sequence 1, 2, 4, 8, 16, 32, 64... holds a profound significance in mathematics, computer science, and even nature itself. This sequence represents the powers of two, a fundamental concept with far-reaching implications. This article delves deep into this fascinating sequence, exploring its mathematical properties, real-world applications, and the broader context of exponential growth. Understanding this sequence is key to unlocking a deeper understanding of many crucial concepts in various fields.
Introduction: The Ubiquitous Powers of Two
The sequence 1, 2, 4, 8, 16, 32, 64... is generated by repeatedly multiplying by two. Each number is double the preceding one. Mathematically, this sequence can be represented as 2<sup>0</sup>, 2<sup>1</sup>, 2<sup>2</sup>, 2<sup>3</sup>, 2<sup>4</sup>, 2<sup>5</sup>, 2<sup>6</sup>, and so on. This simple representation belies the sequence's remarkable importance and its widespread presence across numerous disciplines. From binary code in computers to the branching patterns of trees, the power of two appears again and again, underscoring its fundamental role in our understanding of the world.
Mathematical Properties: Beyond Simple Doubling
While the basic pattern of doubling is straightforward, the mathematical properties of this sequence extend far beyond simple multiplication. Let's explore some key aspects:
-
Exponential Growth: The sequence demonstrates exponential growth, a concept where the rate of increase is proportional to the current value. This differs significantly from linear growth, where the rate of increase remains constant. Exponential growth leads to rapid increases, as seen in the accelerating growth of numbers in the sequence.
-
Geometric Progression: The sequence is a classic example of a geometric progression, a sequence where each term is obtained by multiplying the previous term by a constant value (in this case, 2). Geometric progressions have many interesting properties, including formulas for calculating the sum of a series and identifying patterns.
-
Binary Representation: The powers of two are fundamental to the binary number system, the foundation of digital computing. Binary uses only two digits, 0 and 1, to represent all numbers. Each position in a binary number represents a power of two (e.g., 1011<sub>2</sub> = 12<sup>3</sup> + 02<sup>2</sup> + 12<sup>1</sup> + 12<sup>0</sup> = 11<sub>10</sub>). This is crucial for how computers store and process information.
-
Logarithms Base 2: The logarithm base 2 (log<sub>2</sub>) is the inverse function of 2 raised to the power of x (2<sup>x</sup>). It tells us what power of 2 gives a specific number. For example, log<sub>2</sub>(8) = 3 because 2<sup>3</sup> = 8. Logarithms base 2 are extensively used in computer science, particularly in analyzing algorithm efficiency.
Real-World Applications: From Computing to Nature
The sequence 1, 2, 4, 8, 16, 32, 64... is not just a mathematical curiosity; it has numerous practical applications across various fields:
-
Computer Science: As mentioned earlier, the binary number system, built upon powers of two, is the bedrock of digital computing. Memory allocation, data storage, and many algorithms rely heavily on powers of two. Data structures like binary trees and heaps leverage the properties of this sequence for efficient organization and retrieval.
-
Data Storage: Hard drive capacities, RAM sizes, and other storage units often come in powers of two (e.g., 1GB, 2GB, 4GB, 8GB, etc.) to efficiently utilize the binary system.
-
Networking: Network addresses and subnet masks in IP addressing utilize powers of two for efficient allocation and routing of data packets.
-
Music and Sound: Musical intervals and harmonies are often related to powers of two. An octave represents a doubling of frequency, hence the importance of powers of two in musical theory and acoustics.
-
Biology and Nature: The branching patterns of trees, the arrangement of leaves on a stem, and the spiral patterns in many plants often exhibit Fibonacci numbers and related sequences, which have strong connections to powers of two and exponential growth.
Beyond 64: Exploring the Extrapolation and Limits
While the sequence presented starts with 1, 2, 4, 8, 16, 32, 64, it continues infinitely. The next numbers are 128, 256, 512, 1024, and so on. Each subsequent number represents a significant jump, highlighting the rapid nature of exponential growth. However, this growth is not limitless in practical terms. Physical limitations and the finite nature of resources ultimately constrain the applicability of extremely large powers of two. For example, while we can theoretically talk about 2<sup>100</sup>, representing an astronomically large number, it’s impossible to practically represent or manipulate such a number in most computational contexts.
Understanding Exponential Growth: Implications and Applications
The sequence 1, 2, 4, 8, 16, 32, 64... provides a visual and easily grasped example of exponential growth. Understanding exponential growth is crucial in various contexts:
-
Population Growth: Uncontrolled population growth often follows an exponential pattern, leading to rapid increases in population size.
-
Compound Interest: The power of compound interest, where interest is earned on both the principal and accumulated interest, exemplifies exponential growth. The more time passes, the faster the growth accelerates.
-
Viral Spread: The spread of information, diseases, or trends through social networks or populations often mirrors exponential growth.
-
Technological Advancements: Moore's Law, which states that the number of transistors on a microchip doubles approximately every two years, illustrates exponential growth in computing power.
Frequently Asked Questions (FAQ)
-
Q: What is the formula for the nth term in the sequence?
- A: The formula for the nth term in the sequence 1, 2, 4, 8, 16... is 2<sup>n-1</sup>, where n represents the position of the term in the sequence (starting with n=1).
-
Q: Is there a limit to the sequence?
- A: Mathematically, there is no limit to the sequence, as it can continue infinitely. However, in practical applications, limitations in storage capacity, computational power, or physical resources impose constraints.
-
Q: What is the difference between linear and exponential growth?
- A: Linear growth increases at a constant rate, while exponential growth increases at a rate proportional to the current value. Exponential growth leads to much faster increases over time.
-
Q: How are powers of two used in binary code?
- A: Each digit in a binary number represents a power of two. The rightmost digit represents 2<sup>0</sup> (1), the next represents 2<sup>1</sup> (2), and so on. This allows for a compact representation of numbers using only two digits (0 and 1).
-
Q: Are there any other sequences similar to the powers of two?
- A: Yes, other geometric progressions exist, using different base numbers (e.g., powers of 3, powers of 10). Fibonacci sequence, while not a geometric progression, also shows rapid growth and appears in nature alongside patterns related to powers of two.
Conclusion: The Enduring Relevance of the Power of Two
The seemingly simple sequence 1, 2, 4, 8, 16, 32, 64... unveils a world of mathematical richness and practical applications. From the fundamental workings of computers to the patterns observed in nature, the powers of two play a critical role in shaping our understanding of the world around us. Understanding exponential growth, as exemplified by this sequence, is not just an academic exercise but a vital skill for navigating and interpreting trends in numerous fields, from technology and finance to biology and population studies. The seemingly simple act of repeatedly doubling a number reveals a depth and complexity that continues to inspire awe and further exploration.
Latest Posts
Latest Posts
-
Which Sequence Has A Common Ratio Of 3
Sep 23, 2025
-
1 Kilo Of Rice Is How Many Cups
Sep 23, 2025
-
Choose The Three Parts Of A Nucleotide
Sep 23, 2025
-
How To Find Equation Of A Vertical Line
Sep 23, 2025
-
Common Denominator For 3 4 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 2 4 8 16 32 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.