1/2 + 3/8 In Fraction Form
faraar
Sep 11, 2025 · 6 min read
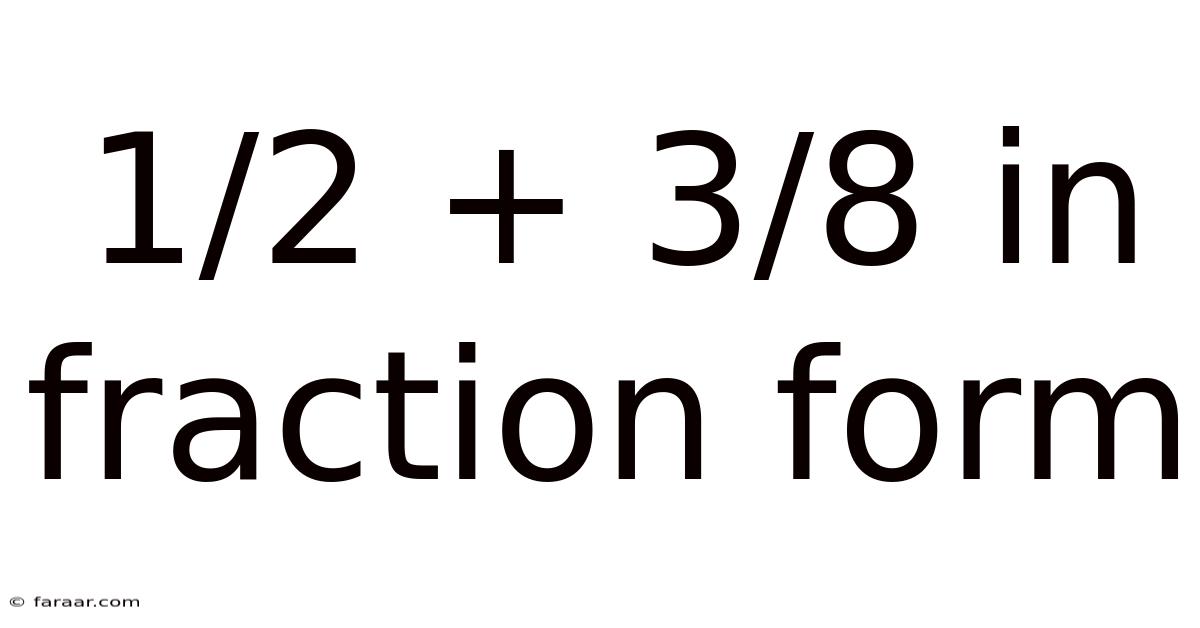
Table of Contents
Mastering Fractions: A Deep Dive into Adding 1/2 + 3/8
Understanding fractions is fundamental to mathematics, forming the bedrock for more advanced concepts. This comprehensive guide will walk you through adding the fractions 1/2 and 3/8, explaining not just the how, but also the why, ensuring you develop a strong grasp of fractional arithmetic. We'll cover the steps involved, the underlying mathematical principles, frequently asked questions, and even explore some real-world applications. By the end, you'll be confident in tackling similar fraction problems independently.
Understanding Fractions: A Quick Refresher
Before diving into the addition, let's solidify our understanding of what fractions represent. A fraction, like 1/2 or 3/8, represents a part of a whole. The number on top, called the numerator, indicates how many parts we have. The number on the bottom, called the denominator, indicates how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) tells us we have one part, and the denominator (2) tells us the whole is divided into two equal parts. Similarly, 3/8 means we have three parts out of a whole divided into eight equal parts.
Adding Fractions: The Common Denominator
The crucial step in adding (or subtracting) fractions is finding a common denominator. This is a number that is a multiple of both denominators. Think of it like this: you can only add apples to apples, not apples to oranges. Similarly, you can only directly add fractions if they have the same denominator.
In our example, we need to find a common denominator for 2 and 8. The multiples of 2 are 2, 4, 6, 8, 10… and the multiples of 8 are 8, 16, 24… Notice that 8 is a multiple of both 2 and 8. Therefore, 8 is our least common denominator (LCD). Using the LCD simplifies calculations and ensures the answer is in its simplest form.
Step-by-Step Solution: 1/2 + 3/8
Now let's add 1/2 and 3/8 step-by-step:
-
Find the common denominator: As determined above, the least common denominator for 2 and 8 is 8.
-
Convert fractions to equivalent fractions with the common denominator: We need to rewrite 1/2 as an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and denominator by the same number (in this case, 4) to maintain the value of the fraction:
(1/2) * (4/4) = 4/8
-
Add the numerators: Now that both fractions have the same denominator, we can simply add their numerators:
4/8 + 3/8 = (4 + 3)/8 = 7/8
-
Simplify (if necessary): In this case, 7/8 is already in its simplest form because 7 and 8 have no common factors other than 1.
Therefore, 1/2 + 3/8 = 7/8.
Visualizing the Addition
Imagine a pizza cut into eight slices. 1/2 of the pizza is four slices (4/8). Adding 3/8 more slices means we now have a total of seven slices (7/8) out of the eight slices. This visual representation helps to solidify the concept and make it more intuitive.
The Mathematical Principles Behind Fraction Addition
The process of adding fractions relies on the fundamental principle of equivalent fractions. Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2, 2/4, 4/8, and so on, are all equivalent fractions.
By finding the common denominator, we are essentially ensuring that we are adding parts of the same size. This allows us to directly add the numerators without altering the overall value of the fractions. This is similar to working with whole numbers where you would align the units, tens and hundreds columns before adding. The common denominator is the equivalent of aligning those columns in a fraction addition.
Extending the Concept: Adding More Than Two Fractions
The method we used to add 1/2 and 3/8 can be extended to add any number of fractions. The key steps remain the same:
-
Find the least common denominator (LCD) of all the denominators. This might require finding the least common multiple (LCM) of the denominators.
-
Convert each fraction to an equivalent fraction with the LCD.
-
Add the numerators.
-
Simplify the resulting fraction to its lowest terms.
Frequently Asked Questions (FAQs)
Q1: What if the fractions don't have a common denominator easily visible?
A: If finding the LCD isn't immediately obvious, you can use the method of finding the prime factorization of each denominator and then taking the highest power of each prime factor. For example, to find the LCD of 6 and 15:
6 = 2 x 3 15 = 3 x 5
The LCD would be 2 x 3 x 5 = 30
Q2: What if the resulting fraction is an improper fraction (numerator is larger than the denominator)?
A: An improper fraction can be converted into a mixed number, which consists of a whole number and a proper fraction. For example, 11/8 can be converted into 1 3/8 (one and three-eighths).
Q3: How can I check my answer?
A: You can estimate the answer. 1/2 is close to 0.5, and 3/8 is close to 0.4. Adding them together is roughly 0.9. 7/8 is approximately 0.875, which is reasonably close to our estimate, confirming our answer is likely correct. You can also use a calculator to verify your result.
Q4: Are there any real-world applications of adding fractions?
A: Absolutely! Adding fractions is used in various real-world situations, such as:
- Cooking and baking: Measuring ingredients often involves fractions.
- Construction and carpentry: Precise measurements in building projects often necessitate fraction arithmetic.
- Sewing and crafting: Cutting fabric or other materials may require calculating fractional lengths.
- Finance: Calculating portions of a budget or dealing with parts of shares often involves fraction manipulation.
Conclusion: Mastering Fractions for a Brighter Future
Adding fractions, while seemingly simple, is a cornerstone of mathematical proficiency. By understanding the underlying principles, practicing the steps, and exploring the real-world applications, you build a solid foundation for more complex mathematical concepts. Remember, the key to mastering fractions lies in grasping the concept of common denominators and equivalent fractions. With consistent practice and attention to detail, you will be able to confidently tackle any fraction addition problem, opening doors to a deeper understanding of mathematics and its practical applications in various fields. So, keep practicing, and remember that even the most complex concepts become manageable with dedicated effort and a clear understanding of the fundamental principles.
Latest Posts
Latest Posts
-
Volume Of A Single Drop Of Water
Sep 11, 2025
-
How To Write A Polynomial Function With Given Zeros
Sep 11, 2025
-
How Do You Find The Mass Of A Solution
Sep 11, 2025
-
What Is 1 2 Of 2 3 Of A Cup
Sep 11, 2025
-
Lead Nitrate And Potassium Iodide Balanced Equation
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 3/8 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.