1/2 + 3/8 How To Solve
faraar
Sep 24, 2025 · 6 min read
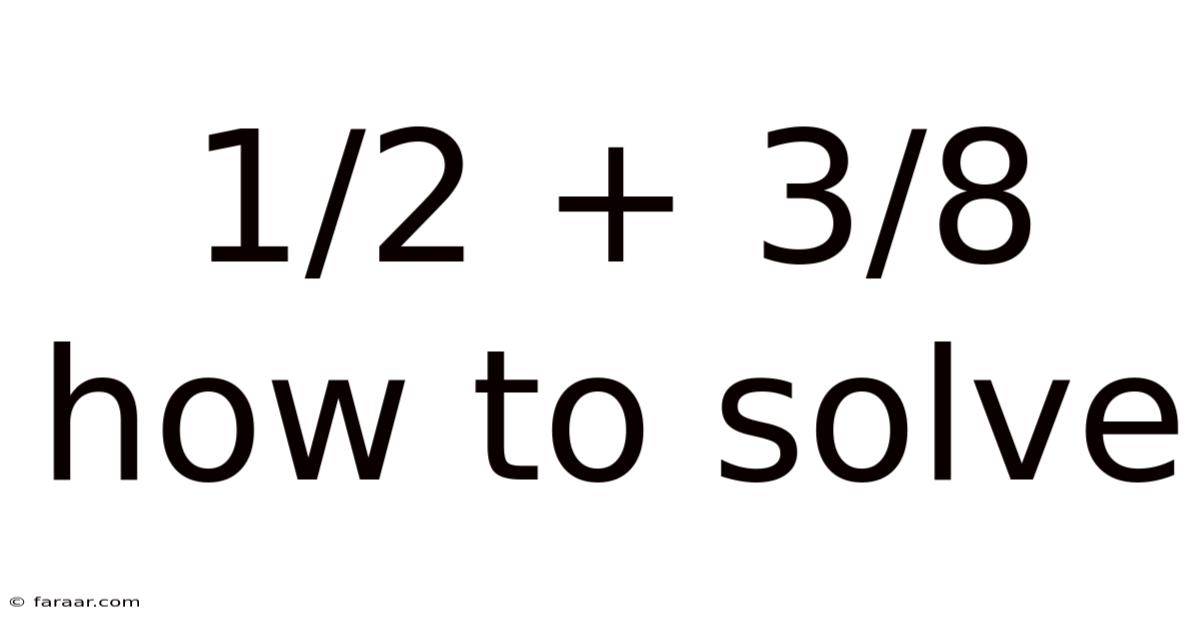
Table of Contents
Mastering Fractions: A Deep Dive into Solving 1/2 + 3/8
Adding fractions might seem simple at first glance, but understanding the underlying principles is crucial for mastering more complex mathematical concepts. This comprehensive guide will walk you through solving the equation 1/2 + 3/8, not just providing the answer, but explaining the why behind each step. We'll explore the fundamental concepts of fractions, delve into the process of finding a common denominator, and finally, solidify your understanding with frequently asked questions and further applications. This guide aims to equip you with the skills to confidently tackle any fraction addition problem you encounter.
Understanding Fractions: A Quick Refresher
Before diving into the solution, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates the whole is divided into two equal parts. Similarly, in 3/8, we have three parts out of a total of eight equal parts.
The Challenge: Solving 1/2 + 3/8
Our task is to add 1/2 and 3/8: 1/2 + 3/8 = ?
The crucial concept here is finding a common denominator. This means finding a number that is divisible by both the denominators of our fractions (2 and 8). Why is this necessary? Because we can only add or subtract fractions when they represent parts of the same sized whole. Think of it like adding apples and oranges – you can't simply say you have 4 "fruit" without specifying how many of each you have.
Finding the Least Common Denominator (LCD)
The easiest way to find the common denominator is to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both numbers.
There are several methods to find the LCM:
-
Listing Multiples: List the multiples of each denominator until you find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12...
- Multiples of 8: 8, 16, 24, 32... The smallest common multiple is 8.
-
Prime Factorization: Break down each denominator into its prime factors. The LCM is found by taking the highest power of each prime factor present in the factorizations.
- 2 = 2
- 8 = 2 x 2 x 2 = 2³ The highest power of 2 is 2³, which is 8.
In this case, the least common denominator (LCD) for 1/2 and 3/8 is 8.
Converting Fractions to a Common Denominator
Now that we have our LCD (8), we need to convert both fractions so they have this denominator. We do this by multiplying both the numerator and the denominator of each fraction by the same number. This doesn't change the value of the fraction, only its representation.
-
Converting 1/2: To change the denominator from 2 to 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
-
Converting 3/8: This fraction already has the denominator 8, so it remains unchanged: 3/8
Adding the Fractions
Now that both fractions have the same denominator (8), we can simply add the numerators and keep the denominator the same:
4/8 + 3/8 = (4 + 3) / 8 = 7/8
Therefore, 1/2 + 3/8 = 7/8
Simplifying Fractions (If Necessary)
Sometimes, after adding fractions, the resulting fraction can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In our case, 7/8 is already in its simplest form because 7 and 8 have no common divisors other than 1.
A Visual Representation
Imagine a pizza cut into 8 slices. 1/2 of the pizza is 4 slices (4/8). If you add 3 more slices (3/8), you have a total of 7 slices out of 8 (7/8).
Explanation using the Number Line
Visualizing fractions on a number line can be helpful. Locate 1/2 and 3/8 on a number line divided into eighths. You'll see that adding them results in a point at 7/8. This provides a geometric interpretation of the addition.
Further Applications and Extensions
The principles of adding fractions extend to more complex scenarios:
-
Adding more than two fractions: Follow the same process – find the LCD for all denominators, convert the fractions, and then add the numerators.
-
Adding mixed numbers: A mixed number contains a whole number and a fraction (e.g., 1 1/2). Convert the mixed numbers to improper fractions (where the numerator is larger than the denominator) before adding them. For example, 1 1/2 becomes 3/2.
-
Subtracting fractions: The process is very similar to addition, but you subtract the numerators instead of adding them.
Frequently Asked Questions (FAQs)
Q: What if the denominators don't share any common factors?
A: If the denominators are relatively prime (meaning they share no common factors other than 1), the LCD will simply be the product of the two denominators. For example, to add 1/3 + 1/5, the LCD would be 15 (3 x 5).
Q: Is there a faster way to find the LCD?
A: While listing multiples works well for smaller numbers, prime factorization is more efficient for larger numbers. For very large numbers, specialized algorithms are used.
Q: Why can't I just add the numerators and the denominators directly?
A: Adding numerators and denominators directly changes the value of the fractions. It's crucial to maintain the proportional relationship between the parts and the whole. Imagine adding 1/2 a cup of sugar to 1/4 a cup of flour. You wouldn't say you have 2/6 of a cup of ingredients.
Q: What if the resulting fraction is an improper fraction (numerator greater than denominator)?
A: You can convert it into a mixed number by performing division. For example, 11/8 can be converted to 1 3/8 (8 goes into 11 once with a remainder of 3).
Conclusion
Adding fractions, while seemingly simple, requires a solid understanding of fundamental concepts. By mastering the techniques of finding the least common denominator, converting fractions, and adding numerators, you'll confidently solve any fraction addition problem. Remember, the key is to visualize the fractions as parts of a whole and to ensure those parts are of the same size before adding them together. This thorough understanding will serve as a strong foundation for more advanced mathematical concepts. Practice regularly and you'll soon find yourself effortlessly solving even the most complex fraction equations.
Latest Posts
Latest Posts
-
0 97 Rounded To The Nearest Tenth
Sep 24, 2025
-
Find The Volume Of The Cone Shown Below
Sep 24, 2025
-
Is This A Dagger Which I See Before Me Meaning
Sep 24, 2025
-
What Is The Density Of Water In G Cm3
Sep 24, 2025
-
How Do Say How Are You In Italian
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 3/8 How To Solve . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.