1/12 Of 1/3 Is What Fraction
faraar
Sep 07, 2025 · 5 min read
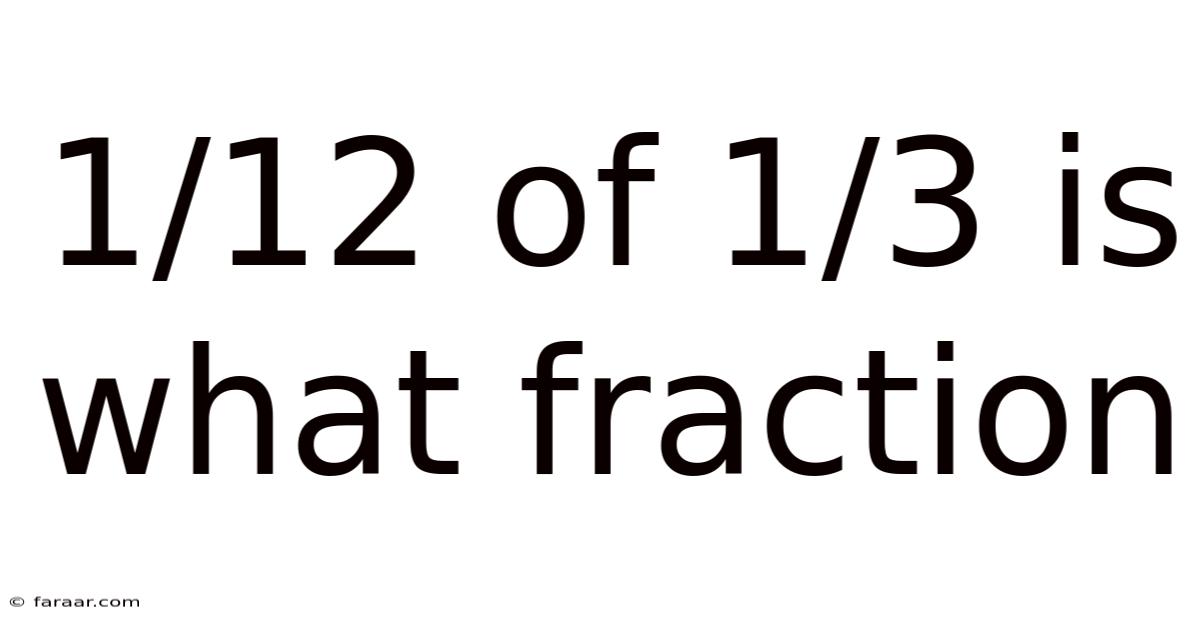
Table of Contents
Decoding Fractions: Understanding 1/12 of 1/3
Finding a fraction of a fraction might seem daunting at first, but with a clear understanding of the process, it becomes surprisingly straightforward. This comprehensive guide will not only answer the question, "1/12 of 1/3 is what fraction?" but also equip you with the knowledge and confidence to tackle similar fraction problems. We'll delve into the step-by-step process, explore the underlying mathematical principles, and address frequently asked questions, ensuring a thorough understanding of this fundamental concept in mathematics.
Understanding the Concept of "Of" in Fractions
Before we dive into the calculation, let's clarify the meaning of "of" when dealing with fractions. In mathematics, "of" signifies multiplication. Therefore, the problem "1/12 of 1/3" translates to 1/12 * 1/3. This simple substitution makes the problem much more manageable.
Step-by-Step Calculation: 1/12 of 1/3
Here's how to calculate 1/12 of 1/3:
-
Rewrite the problem as a multiplication problem: 1/12 x 1/3
-
Multiply the numerators: The numerators are the top numbers in the fractions. In this case, we multiply 1 x 1 = 1.
-
Multiply the denominators: The denominators are the bottom numbers in the fractions. We multiply 12 x 3 = 36.
-
Combine the results: The result of multiplying the numerators becomes the numerator of the answer, and the result of multiplying the denominators becomes the denominator of the answer. This gives us 1/36.
Therefore, 1/12 of 1/3 is 1/36.
Visualizing the Problem
Let's visualize this using a simple example. Imagine a pizza cut into 12 equal slices. 1/12 represents one of those slices. Now, imagine taking one third of that single slice (1/12). To do this, you'd divide that single slice into three equal parts, and you'd be left with one of those three smaller parts. This smaller part represents 1/36 of the whole pizza. This visual representation helps solidify the understanding of the mathematical operation.
The Mathematical Principle Behind Fraction Multiplication
The multiplication of fractions hinges on the concept of finding a portion of a portion. When we multiply two fractions, we're essentially finding a fraction of a fraction, as demonstrated in our pizza example. The process of multiplying numerators and denominators separately is a concise way to represent this operation.
More formally, the multiplication of two fractions a/b and c/d is given by:
(a/b) * (c/d) = (a * c) / (b * d)
Simplifying Fractions
While our answer, 1/36, is already in its simplest form (meaning the numerator and denominator have no common factors other than 1), it's important to know how to simplify fractions. If, for example, we had calculated a result like 4/8, we would need to simplify it. This is done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In the example of 4/8, the GCD is 4, so we divide both the numerator and denominator by 4, resulting in 1/2.
Extending the Concept: Working with More Complex Fractions
The principles discussed above can be applied to more complex fraction problems. For instance, let's consider the problem: (2/5) of (3/7).
-
Rewrite as multiplication: (2/5) x (3/7)
-
Multiply numerators: 2 x 3 = 6
-
Multiply denominators: 5 x 7 = 35
-
Combine: The result is 6/35. This fraction is already in its simplest form.
Mixed Numbers and Fractions
Sometimes, you might encounter problems involving mixed numbers (a whole number and a fraction, like 1 1/2). To multiply fractions involving mixed numbers, you first need to convert the mixed numbers into improper fractions (where the numerator is larger than the denominator). For example, 1 1/2 is equivalent to (1 x 2 + 1)/2 = 3/2. Then, you proceed with the multiplication as shown in previous examples.
Real-World Applications of Fraction Multiplication
Understanding fraction multiplication is crucial in numerous real-world applications. Here are a few examples:
-
Cooking and Baking: Recipes often require fractions of ingredients. Calculating the correct amount when scaling a recipe up or down involves fraction multiplication.
-
Construction and Engineering: Precise measurements and calculations are essential in construction. Fractions are frequently used in blueprints and calculations.
-
Finance: Calculating interest, discounts, and proportions of investments often involves working with fractions.
-
Data Analysis: Representing and analyzing data frequently involves working with percentages and proportions which rely heavily on fractional calculations.
Frequently Asked Questions (FAQ)
Q1: What if I get a fraction that can be simplified?
A1: Always simplify your final answer to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
Q2: Can I use a calculator to solve fraction problems?
A2: Yes, most calculators can handle fraction calculations. However, understanding the underlying principles is essential for problem-solving and building a strong foundation in mathematics. Calculators should be used to verify your work, not to replace your understanding.
Q3: How do I deal with fractions containing decimals?
A3: It's often easier to convert decimals to fractions before performing calculations. For example, 0.5 is equivalent to 1/2.
Q4: What if I have more than two fractions to multiply?
A4: Simply extend the process. Multiply all the numerators together and all the denominators together. Then, simplify the resulting fraction if needed.
Conclusion: Mastering Fractions
Mastering the concept of fraction multiplication, as illustrated by the example of finding 1/12 of 1/3, is a cornerstone of mathematical proficiency. By understanding the underlying principles, following the step-by-step process, and practicing various examples, you'll build confidence and competence in handling fractions effectively. Remember that the key is to break down complex problems into simpler steps and to always simplify your final answer. This knowledge extends far beyond the classroom, proving invaluable in various real-world applications. Keep practicing, and you'll soon find that fractions become far less intimidating!
Latest Posts
Latest Posts
-
3 To The Negative 4th Power
Sep 07, 2025
-
Length Of Diagonal Of A Box
Sep 07, 2025
-
Difference Between Persuasive Essay And Argumentative Essay
Sep 07, 2025
-
What Molecule Absorbs Sunlight For Photosynthesis
Sep 07, 2025
-
What Is The Measure Of Angle Abd
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 1/12 Of 1/3 Is What Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.