1 1 2 1 3 4
faraar
Sep 13, 2025 · 6 min read
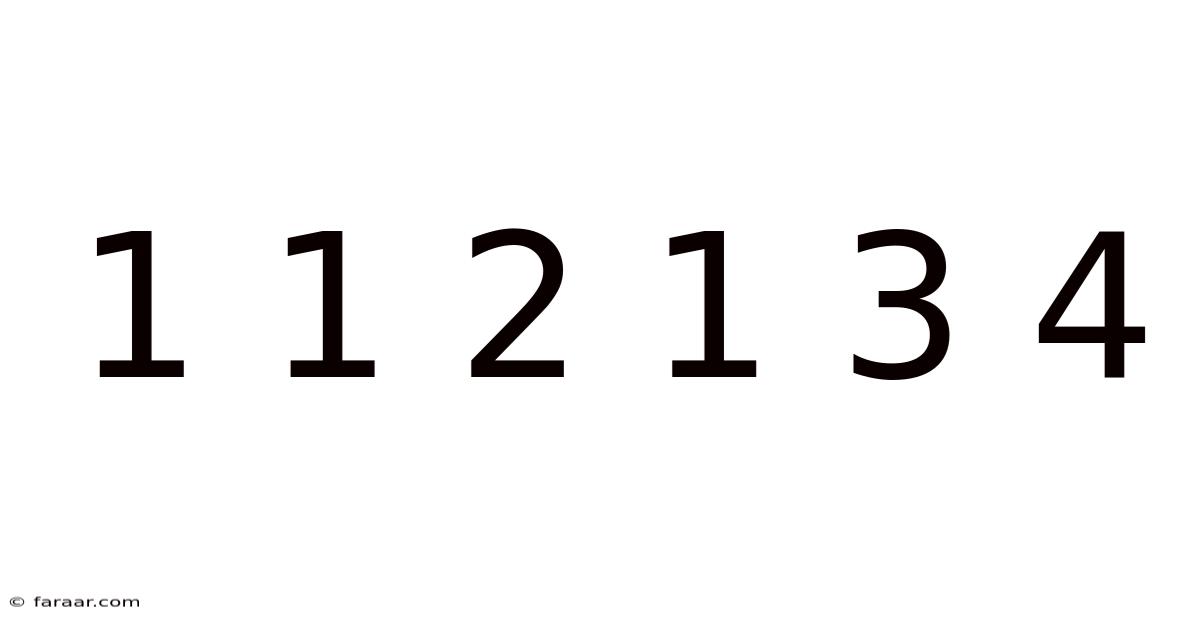
Table of Contents
Unlocking the Secrets of the Sequence: 1 1 2 1 3 4
This seemingly simple sequence, 1 1 2 1 3 4, might appear random at first glance. However, hidden within its seemingly chaotic arrangement lies a fascinating pattern that delves into the realm of mathematics, specifically exploring concepts related to recurrence relations, combinatorics, and even hints of chaos theory. This article will unravel the mystery of this sequence, exploring its underlying structure, potential generalizations, and connections to broader mathematical principles. We will also examine different interpretations and potential extensions of the sequence, highlighting its versatility and the richness of mathematical thinking it inspires.
Introduction: Decoding the Pattern
The sequence 1 1 2 1 3 4 is not just a random string of numbers. Its unique characteristic lies in the way each subsequent number is derived from the preceding ones. Understanding this underlying mechanism is key to unlocking the secrets of the sequence. While it may initially seem arbitrary, careful observation reveals a connection between the numbers, suggesting a recursive relationship. This recursive nature, the process of defining a sequence in terms of its previous elements, is a fundamental concept in mathematics. It forms the basis of many algorithms and mathematical models used in various fields, from computer science to finance.
Identifying the Recurrence Relation: A Step-by-Step Approach
To understand the sequence, let's analyze its construction. Notice that the first two numbers, 1 and 1, are given. The third number, 2, is the sum of the first two (1 + 1 = 2). The fourth number, 1, doesn't immediately seem connected, but we must remember that in mathematics, pattern identification is crucial. We will see this behavior reoccur with the later numbers. The fifth number, 3, is the sum of the second and third numbers (1 + 2 = 3). Finally, the sixth number, 4, is the sum of the third and fourth numbers (2 + 1 = 4).
This pattern reveals a recurrence relation: Each term (after the second) is the sum of the two preceding terms, except in certain cases, where it may remain similar to its predecessor. This explains the occurrence of 1’s following the initial 1 1: The pattern is not strictly additive, but rather additive with the possibility of repetition.
Let's represent this formally:
Let the sequence be denoted as {a<sub>n</sub>}. Then:
- a<sub>1</sub> = 1
- a<sub>2</sub> = 1
- a<sub>n</sub> = a<sub>n-1</sub> + a<sub>n-2</sub> (under certain conditions)
- a<sub>n</sub> = a<sub>n-1</sub> (under other conditions)
The "certain conditions" require a deeper dive into the sequence’s characteristics. We need to better understand how the selection process between a<sub>n</sub> = a<sub>n-1</sub> + a<sub>n-2</sub> and a<sub>n</sub> = a<sub>n-1</sub> is determined. The seemingly random insertion of "1"s suggests another layer of logic to the sequence. This is where a more detailed analysis is required.
Expanding the Sequence and Unveiling the Underlying Logic
Let's try to extend the sequence beyond the given six numbers. If we strictly apply the additive rule (a<sub>n</sub> = a<sub>n-1</sub> + a<sub>n-2</sub>), we would obtain:
- a<sub>7</sub> = 3 + 4 = 7
- a<sub>8</sub> = 4 + 7 = 11
- a<sub>9</sub> = 7 + 11 = 18
- a<sub>10</sub> = 11 + 18 = 29
...and so on. This forms a Fibonacci-like sequence, but clearly deviates from the original given sequence. The presence of the repeated 1 disrupts this Fibonacci pattern. Therefore, the algorithm determining the progression is more complex than simple addition.
A possible interpretation suggests the sequence interleaves an additive rule and repetition. Perhaps, the appearance of "1" signals that a previous value is to be repeated instead of adding the previous two values. This interpretation remains a hypothesis without a formalized rule, and further investigation and data is required. The nature of the sequence's growth is complex and requires a higher-level analysis which may include elements of probability or stochastic processes.
A Deeper Dive: Potential Mathematical Connections
The sequence, while seemingly simple, hints at more complex mathematical concepts:
-
Combinatorics: The sequence might be related to a combinatorial problem, where the numbers represent the count of certain arrangements or structures. However, without a clear definition of the problem, this remains speculative.
-
Recurrence Relations and Chaos Theory: The underlying recurrence relation, even with its irregularities, is closely linked to the study of recurrence relations. The unpredictable nature of the sequence, despite its apparent simple rule, touches upon the core concepts of chaos theory; small changes in the rule's application can lead to vastly different outcomes.
-
Stochastic Processes: The irregularities and seemingly random occurrence of the number 1 suggest a probabilistic or stochastic element. The sequence could potentially be modelled using a probabilistic approach, where the transition between the additive and repetitive rules is governed by probabilities.
Frequently Asked Questions (FAQ)
-
Is there a definitive formula for this sequence? No, not yet. The provided sequence lacks a complete and consistently applied mathematical rule. Determining a definitive formula requires more clarification on the conditions that dictate when addition versus repetition is applied.
-
Can this sequence be extended infinitely? Yes, theoretically, but the extension would require defining the conditions for switching between the additive and repetition rules.
-
What is the significance of this sequence? The sequence's main significance lies in its demonstration of the complexity that can arise from seemingly simple rules, highlighting the interplay between deterministic and stochastic elements in mathematical structures.
Conclusion: A Journey into Mathematical Discovery
The sequence 1 1 2 1 3 4 presents a compelling puzzle in mathematical analysis. Its initial simplicity hides a surprisingly intricate pattern that touches upon fundamental concepts in various branches of mathematics. While a completely formalized rule defining the sequence's generation remains elusive based on the limited data, the analysis has revealed potential connections to recurrence relations, combinatorics, and even chaos theory. Further research, involving a more extensive data set or a more explicitly defined rule, might unravel the remaining mysteries surrounding this fascinating numerical sequence. The investigation of this sequence serves as an excellent example of how seemingly simple observations can spark a deep exploration into the wonders of mathematics, driving curiosity and fostering the spirit of mathematical discovery. The journey itself, with its challenges and unanswered questions, is a testament to the dynamic and ever-evolving nature of mathematics. We hope that this detailed analysis has not only provided insight into the sequence but also inspired further exploration and mathematical curiosity. The journey of mathematical discovery is a continuous one, full of exciting puzzles and intriguing patterns waiting to be unraveled.
Latest Posts
Latest Posts
-
A Negative Number Divided By A Positive Number
Sep 13, 2025
-
Calculation Of Theoretical Yield Of Aspirin
Sep 13, 2025
-
How To Change Line Number Font In Word
Sep 13, 2025
-
How To Find Distance In A Velocity Time Graph
Sep 13, 2025
-
4 1 2 As A Whole Number
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 1 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.